
如图,已知,已知点I是△ABC的内心,射线AI交△ABC的外接圆于点D,交边BC于点E.

(1)ID与BD有何数量关系?为什么?
(2)设△ABC的外接圆半径r=3,ID=2,AD=x,DE=y,当点A在优弧![]() 上运动时,求函数y与自变量x的关系式,并指出自变量的取值范围.
上运动时,求函数y与自变量x的关系式,并指出自变量的取值范围.
|
[答案](1)ID=BD.理由如下: 连接 BI.∵I是△ABC的内心.∴∠1=∠2,∠3=∠4.又∵∠ 5=∠4,∴∠5=∠3.∴∠5+∠2=∠3+∠1,即∠DBI=∠DIB.∴DB=DI.(2)在△ABD和△BDE中, ∵∠ 3=∠5,∠ADB=∠BDE,∴△ABD∽△BDE.∴ ∵ ID=2,AD=x,DE=y.∴xy=4,即y=∵∠ ABD>∠5=∠3,∴AD>BD.又AD≤2R,∴BD<AD≤2R.即2<x≤6.∴自变量 x的取值范围是2<x≤6.[剖析](1)主要考查三角形内心的概念,由于三角形的内心是它的三个角平分线的交点,故连接BI后,会得到∠1=∠2及∠3=∠4.结合圆周角的性质及三角形外角的性质,得到∠DBI=∠DIB,从而得到DI=DB;(2)则寻找三角形相似,运用成比例线段建立x、y之间的关系.由于BD=DI,又BD、DE是△BDE的边,BD、AD是△ABD的边,故不难想到要判断这两个三角形相似. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
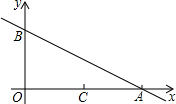 如图,已知点A与点B的坐标分别为(4,0),(0,2).
如图,已知点A与点B的坐标分别为(4,0),(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:
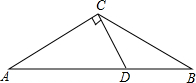 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、观察探索题:
23、观察探索题:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
(2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com