
 如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )
如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )| A. |  | B. | 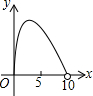 | C. | 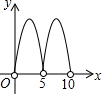 | D. | 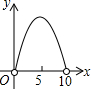 |
分析 按点C在半径OA或半径OB上两种情况分类讨论;首先运用射影定理求出DC的长度,借助矩形的面积公式即可求得y与x的函数关系.
解答  解:根据题意结合图形,分情况讨论:
解:根据题意结合图形,分情况讨论:
如图,①当点C在半径OA上时,连接AD、BD;
∵AB为半圆O的直径,
∴∠ADB=90°,而DC⊥AB,
∴DC2=AC•BC,而AC=x,BC=10-x,
∴DC=$\sqrt{-{x}^{2}+10x}$,而OC=5-x,
∴y=(5-x)$\sqrt{-{x}^{2}+10x}$;
②当点C在半径OB上,即点C′的位置时,
同理可求:y=(x-5)$\sqrt{-{x}^{2}+10x}$,
综上所述,y与x的函数关系式为:
y=$\left\{\begin{array}{l}{(5-x)\sqrt{-{x}^{2}+10x,}(0<x<5)}\\{(x-5)\sqrt{-{x}^{2}+10x,}(5<x<10)}\end{array}\right.$.
所以,y与x之间的函数关系可以用两段二次函数图象表示.
故选:A.
点评 该题主要考查了圆周角定理及其推论、射影定理、矩形的面积公式等几何知识点及其应用问题;作辅助线,牢固掌握圆周角定理及其推论、射影定理等几何知识点是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
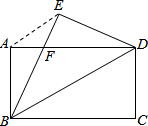 如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com