
【题目】下表记录了一名球员在罚球线上投篮的结果,这么球员投篮一次,投中的概率约是( )
投篮次数 | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数 | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率 | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,联接PA,若AB=4,∠BAD=60°,则PA的最小值是( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() ﹣2 D. 4
﹣2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
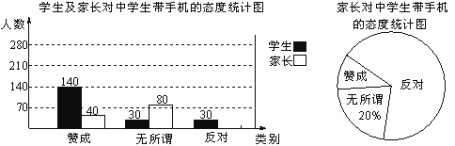
【题目】“校园手机”现象越来越受到社会的关注,小记者张明随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如图所示的统计图:
(1)这次调查的总人数有_____人;
(2)补全两个统计图;
(3)针对随机调查的情况,张明决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小明的家长,小亮和小明的家长被同时选中的概率是_____.(以上三个问题均不需写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
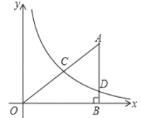
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)设经过C,D两点的一次函数解析式为y1=k1x+b,求出其解析式,并根据图象直接写出在第一象限内,当y1>y时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.

(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
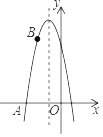
【题目】已知抛物线的对称轴是直线x=﹣1,与x轴一个交点是点A(﹣3,0),且经过点B(﹣2,6)
(1)求该抛物线的解析式;
(2)若点(﹣![]() ,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技实践社团制作实践设备,小明的操作过程如下
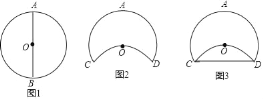
①小明取出老师提供的圆形细铁环,先找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=8分米;
②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2).
③用一细橡胶棒连接C、D两点(如图3);
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为( )
A. 4![]() 分米B. 2
分米B. 2![]() 分米C. 2
分米C. 2![]() 分米D. 3
分米D. 3![]() 分米
分米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com