
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
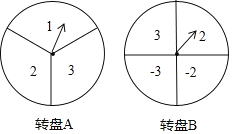
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,G是边AB的中点,平行于AB的动直线l分别交△ABC的边CA、CB于点M、N,设CM=m.
(1)当m=1时,求△MNG的面积;
(2)若点G关于直线l的对称点为点G′,请求出点G′ 恰好落在△ABC的内部(不含边界)时,m的取值范围;
(3)△MNG是否可能为直角三角形?如果能,请求出所有符合条件的m的值;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
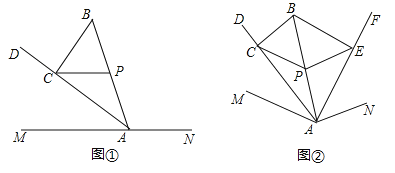
【题目】探究:如图①,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 外,连结
外,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
应用:如图②,点![]() 在
在![]() 内部,连结
内部,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ;作
;作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,则
,则![]() 的大小为多少度.
的大小为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知点![]() 为正方形
为正方形![]() 的对角线的交点,点
的对角线的交点,点![]() 是对角线
是对角线![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 重合),分别过点
重合),分别过点![]() 向直线
向直线![]() 作垂线,垂足分别为点
作垂线,垂足分别为点![]() ,连接
,连接![]() 和
和![]() .
.
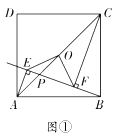

(1)求证:![]() ;
;
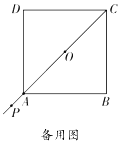
(2)如图②,延长正方形对角线![]() ,当点
,当点![]() 运动到
运动到![]() 的延长线上时,通过证明判断(1)中的结论是否仍然成立;
的延长线上时,通过证明判断(1)中的结论是否仍然成立;
(3)若点![]() 在射线
在射线![]() 上运动,
上运动,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
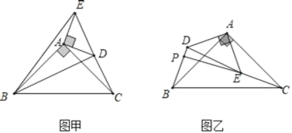
(1)如图甲,将△ADE绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个 .(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若AB=6,AD=3,把△ADE绕点A旋转:
①当∠CAE=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
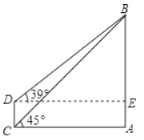
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .
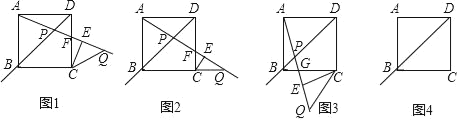
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一放假期间,甲、乙、丙三位同学到某影城看电影,影城有A,B两部不同电影,甲、乙、丙3人分别从中任选一部观看,每部被选中的可能性相同.
(1)甲同学选择“A部电影”的概率为 ;
(2)用画树状图的方法求甲、乙、丙3人选择同一部电影的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com