Question

16．如图1，在坐标系中，A、B在x轴上，C在y轴的正半轴上，且AC⊥BC，CE平分∠ACO，I为△OCB的内心．
（1）求证：BC=BE；
（2）求$\frac{IC}{EC}$的值；
（3）若P（2，-2）在过C、O、B三点的⊙O₁上，如图2，I为△OCB的内心，且IF⊥BC．当⊙O₁变化时，请判断BF-CF的值改变吗？若改变，请说明理由；若不改变，请说明理由，并求出其值．

Answer 1

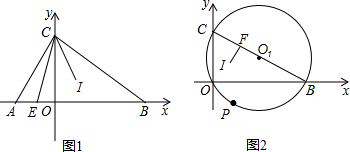
分析 （1）根据内心的概念和三角形的外角的性质证明即可；
（2）连接EI和BI，如图1，易得∠CEO=∠ECB，则有BC=BE，由此可证到△BIE≌△BIC，则有IC=IE，易证∠ECI=45°，即可得到△CEI是等腰直角三角形，就可求出$\frac{IC}{EC}$的z值；
（3）过点I作IM⊥y轴于M，点I作IN⊥x轴于N，连接IC，IO，IB，O₁O，O₁P，如图2，易证△CMI≌△CFI，则有CM=CF．同理可得OM=ON，BN=BF，从而有BF-CF=OB-OC．设点O₁的坐标为（a，b），则OB=2a，OC=2b．根据两点之间距离公式可得a-b=2，就可求出BF-CF的值

解答 （1）证明：∵CE平分∠ACO，
∴∠ACE=∠OCE，
∵AC⊥BC，CO⊥AB，
∴∠A=∠OCB，
∴∠BCE=∠OCE+∠BCO=∠ACE+∠A=∠CEB，
∴BC=BE；
（2）连接EI和BI，如图1，
∵AC⊥BC，即∠ACB=90°，
∴∠CBO+∠CAB=90°．
∵∠BOC=90°，
∴∠CBO+∠BCO=90°，
∴∠CAB=∠BCO．
∵CE平分∠ACO，
∴∠ACE=∠OCE，
∵∠CEO=∠ACE+∠CAB，∠ECB=∠OCE+∠BCO，
∴∠CEO=∠ECB，
∴BC=BE．
∵I为△OCB的内心，
∴∠CBI=∠EBI，
在△BIE和△BIC中，
$\left\{\begin{array}{l}{BC=BE}\\{∠CBI=∠EBI}\\{BI=BI}\end{array}\right.$，
∴△BIE≌△BIC（SAS），
∴IC=IE，
∴∠CEI=∠ECI．
∵CE平分∠ACO，I为△OCB的内心，
∴∠ECI=$\frac{1}{2}$∠ACO+$\frac{1}{2}$∠BCO=$\frac{1}{2}$∠ACB=45°，
∴∠CEI=45°，∠CIE=90°，
∴sin45°=$\frac{IC}{EC}$=$\frac{\sqrt{2}}{2}$；
（3）过点I作IM⊥y轴于M，点I作IN⊥x轴于N，连接IC，IO，IB，O₁O，O₁P，如图2．
∵I为△OCB的内心，
∴∠MCI=∠FCI．
在△CMI和△CFI中，
$\left\{\begin{array}{l}{∠MCI=∠FCI}\\{∠CMI=∠CFI}\\{CI=CI}\end{array}\right.$，
∴△CMI≌△CFI，
∴CM=CF．
同理可得：OM=ON，BN=BF，
∴BF-CF=BN-CM=OB-OC．
设点O₁的坐标为（a，b），
则OB=2a，OC=2b．
∵P（2，-2），O（0，0），O₁P=O₁O，
∴根据两点之间距离公式可得：
（a-2）²+（b+2）²=（a-0）²+（b-0）²，
整理得a-b=2，
∴BF-CF=2a-2b=2（a-b）=4．
∴BF-CF的值为4．

点评 本题主要考查了直角三角形两锐角互余、三角形外角的性质、同角的余角相等、全等三角形的判定与性质、等腰三角形的判定与性质、两点之间距离公式、三角形的内心、特殊角的三角函数值等知识，综合性比较强，把BF-CF转化为OB-OC，并运用两点之间距离公式是解决第（2）小题的关键．