
【题目】2020年1月份,为抗击新型冠状病毒,某药店计划购进一批甲、乙两种型号的口罩,已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元,用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同.
(1)求每袋甲种、乙种口罩的进价分别是多少元?
(2)该药店计划购进甲、乙两种口罩共480袋,其中甲种口罩的袋数少于乙种口罩袋数的![]() ,药店决定此次进货的总资金不超过10000元,求商场共有几种进货方案?
,药店决定此次进货的总资金不超过10000元,求商场共有几种进货方案?
【答案】(1)甲,乙两种口罩分别是15元/件,25元/件;(2)共有4种方案.
【解析】
(1)分别设出甲、乙两种口罩的进价,根据“用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同”列出方程,检验即可得出答案;
(2)设购进甲种口罩y件,则购进乙种口罩(480﹣y)件,根据“甲种口罩的袋数少于乙种口罩袋数的![]() ,药店决定此次进货的总资金不超过10000元”列出不等式组,解不等式组即可得出答案.
,药店决定此次进货的总资金不超过10000元”列出不等式组,解不等式组即可得出答案.
解:(1)设甲种口罩进价x元/件,则乙种口罩进价为(40﹣x)元/件,![]() x=15,经检验x=15是原方程的解.∴40﹣x=25.
x=15,经检验x=15是原方程的解.∴40﹣x=25.
答:甲,乙两种口罩分别是15元/件,25元/件;
(2)设购进甲种口罩y件,则购进乙种口罩(480﹣y)件,
则 ,
,
解得200≤y<204.
因为y是整数,甲种口罩的件数少于乙种口罩的件数,
∴y取200,201,202,203,共有4种方案.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
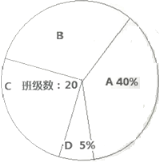
【题目】为了弘扬传统文化,提高学生文明意识,育才学校组织全校80个班级进行"诵经典,传文明"表演赛,比赛后对各班成绩进行了整理,分成4个小组(![]() 表示成绩,单位:分),并根据成绩设立了特等奖、一等奖、二等奖和三等奖.
表示成绩,单位:分),并根据成绩设立了特等奖、一等奖、二等奖和三等奖.![]() 组(三等奖):
组(三等奖):![]() ;
;![]() 组(二等奖):
组(二等奖):![]() ;
;![]() 组(一等奖):
组(一等奖):![]() ;
;![]() 组(特等奖):
组(特等奖):![]() .并绘制如下不完整的扇形统计图.
.并绘制如下不完整的扇形统计图.
请根据图中信息,解答下列问题:
(1)求扇形统计图中,![]() 组对应的圆心角是多少度?
组对应的圆心角是多少度?
(2)学校从获得特等奖的班级中选取了2名男生和2名女生组成代表队参加了区级比赛,由于表现突出,被要求再从这4名学生中随机选取两名同学参加市级比赛,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
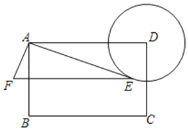
【题目】如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=![]() ,则点F与点C的最小距离为_____.
,则点F与点C的最小距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
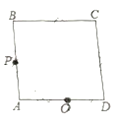
【题目】如图,已知正方形ABCD的边长为8,点O是AD上一个定点,A0=5,点P从点A出发,以每秒1个单位长的速度,按照A-B-C-D的方向,在正方形的边上运动,设运动的时间为1 (秒),当t的值为________时, △AOP是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
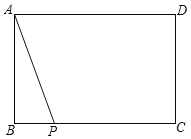
【题目】如图,已知矩形ABCD中,AB=3,BC=5,P是线段BC上的一动点.
(1)请用不带刻度的直尺和圆规,按下列要求作图:(不要求写作法,但保留作图痕迹),在CD边上确定一点E,使得∠DEP+∠APB=180°;
(2)在(1)的条件下,点P从点B移动到点C的过程中,对应点E随之运动,则移动过程中点E经过的总路程长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“伴随点”.
,那么称点Q为点P的“伴随点”.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).
(1)直接写出点A(2,1)的“伴随点”A′的坐标.
(2)点B(m,m+1)在函数y=kx+3的图象上,若其“伴随点”B′的纵坐标为2,求函数y=kx+3的解析式.
(3)点C、D在函数y=﹣x2+4的图象上,且点C、D关于y轴对称,点D的“伴随点”为D′.若点C在第一象限,且CD=DD′,求此时“伴随点”D′的横坐标.
(4)点E在函数y=﹣x2+n(﹣1≤x≤2)的图象上,若其“伴随点”E′的纵坐标y′的最大值为m(1≤m≤3),直接写出实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com