
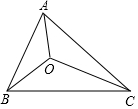
 如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5.
如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5. 分析 首先过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,由OA,OB,OC是△ABC的三条角平分线,根据角平分线的性质,可得OD=OE=OF,又由△ABC的三边AB、BC、CA长分别为40、50、60,即可求得S△ABO:S△BCO:S△CAO的值.
解答  解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=($\frac{1}{2}$AB•OD):($\frac{1}{2}$BC•OF):($\frac{1}{2}$AC•OE)=AB:BC:AC=40:50:60=4:5:6.
故答案为:4:5:6.
点评 此题考查了角平分线的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:填空题
| 试验种子数n(粒) | 1 | 5 | 50 | 200 | 500 | 1000 | 3000 |
| 发芽频数m | 0 | 4 | 45 | 188 | 476 | 951 | 2850 |
| 发芽频率$\frac{m}{n}$ | 0 | 0.8 | 0.9 | 0.94 | 0.952 | 0.951 | 0.95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com