
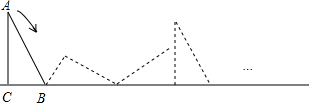
分析 根据含30°的直角三角形三边的关系得到BC=1,AB=2BC=2,∠ABC=60°;点A先以B点为旋转中心,顺时针旋转120°到A1,再以点C1为旋转中心,顺时针旋转90°到A2,然后根据弧长公式计算两段弧长,从而得到点A第4次落在直线l上时,点A所经过的路线的长.
解答 解:∵Rt△ABC中,AC=$\sqrt{3}$,∠ACB=90°,∠A=30°,
∴BC=1,AB=2BC=2,∠ABC=60°;
∵Rt△ABC由现在的位置向右无滑动的翻转,且点A第3次落在直线l上时,有4个$\widehat{A{A}_{1}}$的长,3个$\widehat{{A}_{1}{A}_{2}}$的长,
∴点A经过的路线长=$\frac{120•π•2}{180}$×4+$\frac{90•π•\sqrt{3}}{180}$×3=($\frac{16}{3}$+$\frac{3\sqrt{3}}{2}$)π,
故答案为:($\frac{16}{3}$+$\frac{3\sqrt{3}}{2}$)π.
点评 本题考查了弧长公式:l=$\frac{nπr}{180}$(其中n为圆心角的度数,r为半径);也考查了旋转的性质以及含30度的直角三角形三边的关系.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-1 | B. | x≥-1且x≠2 | C. | x≠2 | D. | x>-1且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -7,18,-9,-15的代数和 | B. | -7加18减-9减15 | ||
| C. | -7加18加+9加+15 | D. | -7减18减9减-15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于正半轴 | ||
| C. | 抛物线与x轴有两个交点 | D. | y有最大值,为-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com