
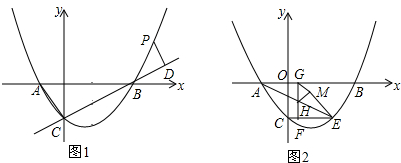
���� ��1���������B���꣬�ڽ�϶Գ�����������߽���ʽ���ɣ�
��2�������ֱ��BP�Ľ���ʽ�������������ߣ��ⷽ���鼴�ɣ�
��3�������F���꣬��ʾ��H���꣬��һ����ʾ�߶�GH��HF��HM�ij��ȣ���������֣�GH=GM��GH=HM��GM=NM������̸�ۼ��ɣ�
��� �⣺��1����ֱ��y=$\frac{1}{2}x-4$��x���ϵĵ�B��
���B������8��0����
����������x�ύ�ڵ�A��B�����ҶԳ���Ϊ��x=$\frac{5}{2}$��
���A������-3��0����
�������ߵĽ���ʽΪ��y=$\frac{1}{6}{x}^{2}-\frac{5}{6}x-4$��
��2����ͼ1
y=$\frac{1}{6}{x}^{2}-\frac{5}{6}x-4$����x=0����ã�y=-4��
���C��0��-4����
����OC=4��0A=3��OB=8��
�ߡ�PBD=��ACO
��tan��PBD=tan��ACO=$\frac{3}{4}$��
�ߡ�DBx=��ABC��
��tan��DBx=tan��ABC=$\frac{1}{2}$��
��tan��PBx=$\frac{\frac{3}{4}+\frac{1}{2}}{1-\frac{3}{4}��\frac{1}{2}}$=2��
����ֱ��BP��y=2x+n��
�ѵ�B��8��0�����룬��ã�n=-16��
��ֱ��BP��y=2x-16��
����$\left\{\begin{array}{l}{y=2x-16}\\{y=\frac{1}{6}{x}^{2}-\frac{5}{6}x-4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=8}\\{y=0}\end{array}\right.$����$\left\{\begin{array}{l}{x=9}\\{y=2}\end{array}\right.$��
���Ե�P����Ϊ����9��2����
��3����ͼ2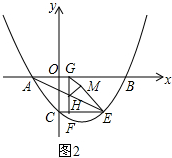
��CE��x�ύ�������ڵ�E�������ߵĶԳ�����ֱ��x=$\frac{5}{2}$���ɵã���E��5��-4����
��A��-3��0�����������㷨����ֱ��AE�Ľ���ʽΪ��y=-$\frac{1}{2}x-\frac{3}{2}$��
���F��m��4����
���H��m��$-\frac{1}{2}m-\frac{3}{2}$����
��GH=$\frac{1}{2}m+\frac{3}{2}$��HF=$-\frac{1}{2}m+\frac{5}{2}$��
������ɵã�HM=HF=$-\frac{1}{2}m+\frac{5}{2}$��
��CEH=��HEM��
��tan��CEH=$\frac{OC}{CE}$=$\frac{1}{2}$��
��tan��CEM=$\frac{2��\frac{1}{2}}{1-��\frac{1}{2}��^{2}}$=$\frac{4}{3}$��
�������֤����GHM=��CEM��
��tan��GHM=$\frac{4}{3}$��cos��GHM=$\frac{3}{5}$��
��GH=HMʱ��GH=HF��
��$\frac{1}{2}m+\frac{3}{2}$=$-\frac{1}{2}m+\frac{5}{2}$��
��ã�m=1��EF=5-1=4��
��GM=HMʱ��cos��GHM=$\frac{\frac{1}{2}GH}{HM}$=$\frac{\frac{1}{4}m+\frac{3}{4}}{-\frac{1}{2}m+\frac{5}{2}}$=$\frac{3}{5}$��
��ã�m=$\frac{15}{11}$����ʱEF=5-$\frac{15}{11}$=$\frac{40}{11}$��
��GH=GMʱ��cos��GHM=$\frac{\frac{1}{2}HM}{GH}$=$\frac{-\frac{1}{4}m+\frac{5}{4}}{\frac{1}{2}m+\frac{3}{2}}$=$\frac{3}{5}$��
��ã�m=$\frac{7}{11}$����ʱ��EF=5-$\frac{7}{11}$=$\frac{48}{11}$��
���� ������Ҫ������κ������ۺ����⣬��������ͽ���ʽ�������������鲢ȷ��⣬��������۵����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����P��ֱ��l��y=-2x-2�ϵĵ㣬����P����һ��ֱ��m��������y=x2��A��B���㣬��֤��������ֱ��l�����������һ��P�����������϶����ҵ���A��ʹ��PA=AB������
��ͼ����P��ֱ��l��y=-2x-2�ϵĵ㣬����P����һ��ֱ��m��������y=x2��A��B���㣬��֤��������ֱ��l�����������һ��P�����������϶����ҵ���A��ʹ��PA=AB�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
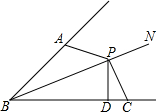 ��֪��ͼ����ABP=��CBP��PΪBN��һ�㣬��PD��BC�ڵ�D����BAP+��BCP=180�㣬��֤��AB+BC=2BD��
��֪��ͼ����ABP=��CBP��PΪBN��һ�㣬��PD��BC�ڵ�D����BAP+��BCP=180�㣬��֤��AB+BC=2BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com