
【题目】已知![]() 和
和![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在射线
在射线![]() 上.
上.

(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC. .
【答案】(1)见解析;(2)见解析;
【解析】
(1)由∠BAC=∠EDF=60°,推出△ABC、△DEF为等边三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根据全等三角形的性质得到AD=BE,即可得到结论;
(2)在FA上截取FM=AE,连接DM,推出△AED≌△MFD(SAS),根据全等三角形的性质得到DA=DM=AB=AC,∠ADE=∠MDF,证得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根据全等三角形的性质得到AM=BC,即可得到结论.
证明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中

∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,连接DM,
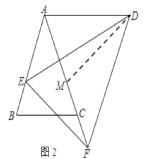
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
在△AED和△MFD中
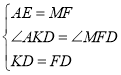 ,
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,
 ,
,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.


科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.
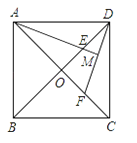
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE分别交边AB、AC于点E、D.

(1)若∠A=40°,求∠DBC的度数;
(2)若△BCD的周长为8,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com