
如图,直线y=2x+2与y轴交于A点,与反比例函数 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.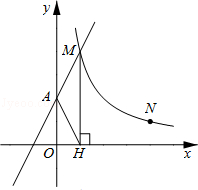
解:(1)由y=2x+2可知A(0,2),即OA=2。
∵tan∠AHO=2,∴OH=1。
∵MH⊥x轴,∴点M的横坐标为1。
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4)。
∵点M在 上,∴k=1×4=4。
上,∴k=1×4=4。
(2)存在。
∵点N(a,1)在反比例函数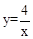 (x>0)上,
(x>0)上,
∴a=4.即点N的坐标为(4,1)。
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示)。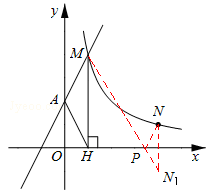
此时PM+PN最小。
∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1)。
设直线MN1的解析式为y=kx+b。
由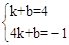 解得
解得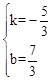 。
。
∴直线MN1的解析式为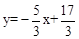 。
。
令y=0,得x=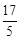 .
.
∴P点坐标为(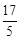 ,0)。
,0)。
解析


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
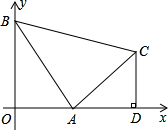 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 | x |
 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com