练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知四边形ABCD是矩形,O是对角线的交点.图中共有几对三角形全等?并选择一对加以证明.

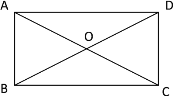
    （1）有________对.

    （2）证明:

    【答案】（1）8；（2）见解析.

    【解析】

    （1）根据矩形的性质和全等三角形的性质可得答案；

    （2）根据SSS可直接证明△ABD≌△CDB.

    （1）根据矩形的性质和全等三角形的性质可知，有△AOB≌△DOC，△AOD≌△BOC，△ABD≌△DCA，△ABD≌△CDB，△ABD≌△BAC，△DCA≌△CDB，△DCA≌△BAC，△CDB≌△BAC，共8对，

    故答案为：8；

    （2）△ABD≌△CDB，

    证明：∵四边形ABCD是矩形，

    ∴AB=CD，AD=BC，

    又∵BD=DB，

    ∴△ABD≌△CDB（SSS）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

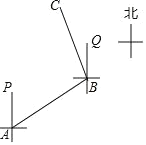
    【题目】为全力推进农村公路快速发展，解决农村“出行难”问题，现将 A、B、C 三村连通的公路进行硬化改造(如图所示)，铺设成水泥路面．已知 B 村在 A 村的北偏东 60°方向上，∠ABC＝110°．

    (1)C 村在 B 村的什么方向上？

    (2)甲、乙两个施工队分别从 A 村、C 村向 B 村施工，两队的施工进度相同A 村到 B 村的距离比 C 到 B 村的距离多 400 米，甲队用了 9 天完成铺设任务乙队用了 7 天完成铺设任务，求两段公路的总长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E，F分别是BC，CD上的点．且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系并证明． (提示：延长CD到G，使得DG＝BE)

    (2)如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；

    (3)如图3，在某次军事演习中，舰艇甲在指挥中心(O处)北偏西20°的A处，舰艇乙在指挥中心南偏东60°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．(可利用(2)的结论)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若将一幅三角板按如图所示的方式放置，则下列结论中不正确的是( )

    A. ∠1＝∠3 B. 如果∠2＝30°，则有AC∥DE

    C. 如果∠2＝30°，则有BC∥AD D. 如果∠2＝30°，必有∠4＝∠C

    查看答案和解析>>

    科目：初中数学 来源： 题型：

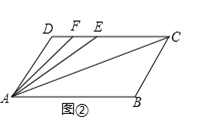
    【题目】如图①，已知AD∥BC，∠B=∠D=120°．

    （1）请问：AB与CD平行吗？为什么？

    （2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．

    （3）若点E在直线CD上，且满足∠EAC=∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某花店准备购进甲、乙两种花卉，若购进甲种花卉20盆，乙种花卉50盆，需要720元；若购进甲种花卉40盆，乙种花卉30盆，需要880元．

    （1）求购进甲、乙两种花卉，每盆各需多少元？

    （2）该花店销售甲种花卉每盆可获利6元，销售乙种花卉每盆可获利1元，现该花店准备拿出800元全部用来购进这两种花卉，设购进甲种花卉m盆，求当m的值等于40时，两种花卉全部销售后获得的利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一长，宽的长方形纸板，现要求以其一组对边中点所在直线为轴，旋转，得到一个几何体（结果保留）；

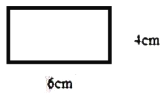
    （1）写出该几何体的名称__________；

    （2）所构造的圆柱体的侧面积__________；

    （3）求所构造的圆柱体的体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按元销售时，每天可销售个；若销售单价每降低元，每天可多售出个.已知每个玩具的固定成本为元，问这种玩具的销售单价为多少元时，厂家每天可获利润元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点、、是数轴上三点，点表示的数为， ， ．

    （）写出数轴上点、表示的数：__________，__________．

    （）动点， 同时从， 出发，点以每秒个单位长度的速度沿数轴向右匀速运动，点以个单位长度的速度沿数向左匀速运动，设运动时间为秒．

    ①求数轴上点， 表示的数（用含的式子表示）；

    ②为何值时，点， 相距个单位长度．

    查看答案和解析>>

    同步练习册答案