
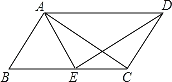
【题目】如图,在ABCD中,AB=AE.
(1)求证:AC=ED;
(2)若AE平分∠DAB,∠EAC=25°.求∠ACD的度数.
【答案】(1)见解析;(2)85°
【解析】
(1)△ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明![]() ABC≌
ABC≌![]() EAD(SAS),进而得出答案;
EAD(SAS),进而得出答案;
(2)先证明![]() ABE为等边三角形,利用平行四边形的性质求解即可.
ABE为等边三角形,利用平行四边形的性质求解即可.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
在△ABC和△AED中,
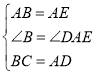 ,
,
∴![]() ABC≌
ABC≌![]() EAD(SAS),
EAD(SAS),
∴AC=ED.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,∠AEB=∠B.
∴∠BAE=∠AEB=∠B.
∴![]() ABE为等边三角形.
ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∴∠ACD=∠BAC=85°.


科目:初中数学 来源: 题型:
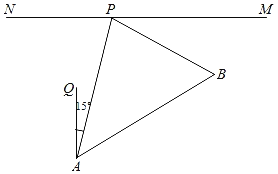
【题目】如图,在一条东西走向的公路MN的同侧有A,B两个村庄,村庄B位于村庄A的北偏东60°的方向上(∠QAB=60°),公路旁的货站P位于村庄A的北偏东15°的方向上,已知PA平分∠BPN,AP=2km,求村庄A,B之间的距离.(计算结果精确到0.01km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
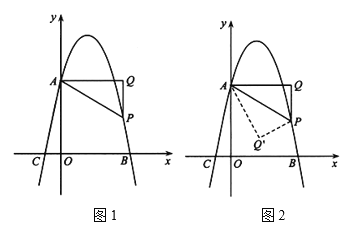
【题目】如图1,已知抛物线![]() 交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作
交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作![]() 于点Q,连接AP(AP不平行x轴).
于点Q,连接AP(AP不平行x轴).
(1)求抛物线的解析式;
(2)点P在抛物线上运动,若![]() ∽
∽![]() (点P与点C对应),求点P的坐标;
(点P与点C对应),求点P的坐标;
(3)如图2,若点P位于抛物线的对称轴的右侧,将![]() 沿AP对折,点Q的对应点为点
沿AP对折,点Q的对应点为点![]() ,当点
,当点![]() 落在x轴上时,求点P的坐标.
落在x轴上时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 、正方形
、正方形![]() 如图放置,点
如图放置,点![]() 在同一条直线上,点
在同一条直线上,点![]() 在
在![]() 边上,
边上,![]() ,且
,且![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .以上结论正确的个数有( )
.以上结论正确的个数有( )
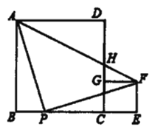
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(注:凸四边形就是没有角度数大于180°的四边形,把四边形的任何一边向两方延长,其他各边都在延长所得直线的同一旁,这样的四边形叫做凸四边形.)

(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有_________;②在凸四边形![]() 中,
中,![]() 且
且![]() ,则该四边形_________“十字形”.(填“是”或“不是”)
,则该四边形_________“十字形”.(填“是”或“不是”)
(2)如图1,![]() ,
,![]() ,
,![]() ,
,![]() 是半径为1的
是半径为1的![]() 上按逆时针方向排列的四个动点,
上按逆时针方向排列的四个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图2,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() ,
,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线与
是抛物线与![]() 轴的交点,点
轴的交点,点![]() 的坐标为
的坐标为![]() ,记“十字形”
,记“十字形”![]() 的面积为
的面积为![]() ,记
,记![]() ,
,![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() .求同时满足下列三个条件的抛物线的解析式:①
.求同时满足下列三个条件的抛物线的解析式:①![]() ;②
;②![]() ;③“十字形”
;③“十字形”![]() 的周长为
的周长为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
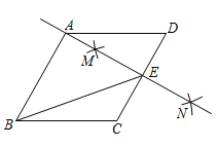
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
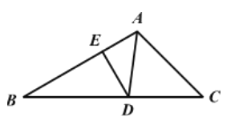
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com