
��ͼ��ʾ��OB�ǡ�AOC��ƽ���ߣ�OD�ǡ�COE��ƽ���ߣ�
(1)����AOB��50�㣬��DOE��35�㣬���BOD�Ķ�����
(2)����AOE��160�㣬��COD��40�㣬���AOB�Ķ�����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ������
(8��)�ⷽ�̣�
(1)2(x��3)����3(x��1)��2; (2) 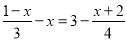 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
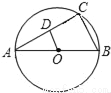
��ͼ����֪ABΪ��O��ֱ����ACΪ�ң�OD��BC����AC��D��BC=4cm��
��1����֤��AC��OD��
��2����OD�ij���
��3����2sinA��1=0�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
һ�˳�ѩ�����±�1��  ��б�±�ֱ���£����µľ���s��m����ʱ��t��s����Ĺ�ϵΪs=10t+2t2���������µ�ʱ��Ϊ4s��������½��ĸ߶�Ϊ��������
��б�±�ֱ���£����µľ���s��m����ʱ��t��s����Ĺ�ϵΪs=10t+2t2���������µ�ʱ��Ϊ4s��������½��ĸ߶�Ϊ��������

A. 72m B. 36 m C. 36m D. 18
m C. 36m D. 18 m
m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
��ͼ����AB��OC������Ϊ��C������OA����OC��2��AB��4����OA���ڣ� ��

A. 2 B. 2
B. 2 C. 3
C. 3 D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ������
��ͼ��OA�ķ����DZ�ƫ��15�㣬OB�ķ����DZ�ƫ��40�㣬����AOC����AOB����OC�ķ�����__

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ������OA��OB��ʾͬһ�����ߵ���(����)

A. ��A�� B. ��B�� C. ��C�� D. ��D��
B �����������������A�������෴����A����ͬһ�����ߣ� B���˵���ͬ��������ͬ����C��ͬһ�����ߣ� C������ͬ����D����ͬһ�����ߣ� D�������෴����B����ͬһ�����ߣ� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��ͼ����ABC�ա� �����С�A=36��,��C=24�㣬���B=_____ .
�����С�A=36��,��C=24�㣬���B=_____ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
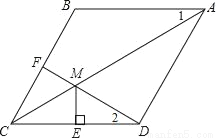
��֪����ͼ��������ABCD�У�FΪ��BC���е㣬DF��Խ���AC���ڵ�M����M��ME��CD�ڵ�E����1=��2��
��1����CE=1����BC�ij���
��2����֤��AM=DF+ME��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com