
分析 分别解出|$\frac{2}{5}$x-1|<4、|$\frac{2}{5}$x-1|≥1的解集,再求公共部分即可.
解答 解:1≤|$\frac{2}{5}$x-1|<4即为
|$\frac{2}{5}$x-1|<4且|$\frac{2}{5}$x-1|≥1,
即有$\left\{\begin{array}{l}{-4<\frac{2}{5}x-1<4}\\{\frac{2}{5}x-1≥1或\frac{2}{5}x-1≤-1}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{15}{2}<x<\frac{25}{2}}\\{x≥5或x≤0}\end{array}\right.$,
即有5≤x<$\frac{25}{2}$或$-\frac{15}{2}$<x≤0.
则解集为5≤x<$\frac{25}{2}$或$-\frac{15}{2}$<x≤0.
点评 本题考查绝对值不等式的解法,关键是根据绝对值不等式的解集进行分析.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.
如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
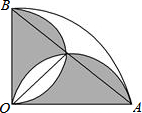 半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.
半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com