
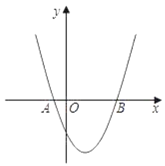
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)若p为x轴上方抛物线上一点,且三角形PAB面积为20,求P点坐标.
【答案】(1)y=x2﹣2x﹣3, (1,﹣4);(2)P点的坐标为(1+![]() ,10)或(1﹣
,10)或(1﹣![]() ,10)
,10)
【解析】
(1)利用待定系数法求解即可;
(2)设P点的纵坐标为n(n>0),由![]() =20,解得n=10,即可得到方程x2﹣2x﹣3=10,求解即可得到点P的坐标.
=20,解得n=10,即可得到方程x2﹣2x﹣3=10,求解即可得到点P的坐标.
解:(1)∵抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4);
(2)设P点的纵坐标为n(n>0),
∵A(﹣1,0)、B(3,0),
∴AB=4,
∴![]() =20,解得n=10,
=20,解得n=10,
把y=10代入y=x2﹣2x﹣3得,x2﹣2x﹣3=10,
解得x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
∴P点的坐标为(1+![]() ,10)或(1﹣
,10)或(1﹣![]() ,10).
,10).


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
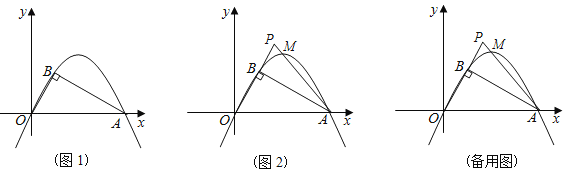
【题目】如图1,抛物线y=ax2+bx经过原点O和点A(12,0),在B在抛物线上,已知OB⊥BA,且∠A=30°.
(1)求此抛物线的解析式.
(2)如图2,点P为OB延长线上一点,若连接AP交抛物线于点M,设点P的横坐标为t,点M的横坐标为m,试用含有t的代数式表示m,不要求写取值范围.
(3)在(2)的条件下,过点O作OW⊥AP于W,并交线段AB于点G,过点W的直线交OP延长线于点N,交x轴于点K,若∠WKA=2∠OAP,且NK=11,求点M的横坐标及WG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
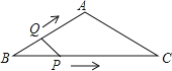
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
A.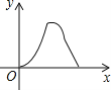 B.
B.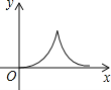 C.
C.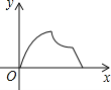 D.
D.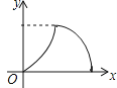
查看答案和解析>>
科目:初中数学 来源: 题型:
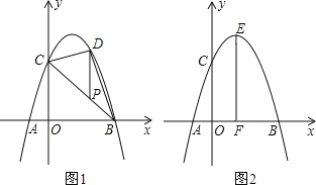
【题目】 在平面直角坐标系中,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;
(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+![]() MB的最小值以及此时点M、N的坐标.
MB的最小值以及此时点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
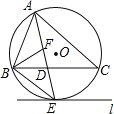
【题目】如图,圆O是![]() 的外接圆,AE平分
的外接圆,AE平分![]() 交圆O于点E,交BC于点D,过点E作直线
交圆O于点E,交BC于点D,过点E作直线![]() .
.
(1)判断直线l与圆O的关系,并说明理由;
(2)若![]() 的平分线BF交AD于点F,求证:
的平分线BF交AD于点F,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点横坐标是2,与x轴交于A(x1,0)、
图象的顶点横坐标是2,与x轴交于A(x1,0)、
B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,![]() .
.
(1)求证:![]() ;
;
(2)求m、n的值;
(3)当p﹥0且二次函数图象与直线![]() 仅有一个交点时,求二次函数的最大值.
仅有一个交点时,求二次函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 30 | 40 | 60 |
周销售量y(件) | 90 | 70 | 30 |
周销售利润w(元) | 450 | 1050 | 1050 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)当售价定为多少时,周销售利润最大,最大利润是多少?
(3)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过45元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1080元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com