
如图所示,已知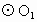 与
与 相交于B、C,AB是
相交于B、C,AB是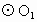 的直径,AB、AC的延长线分别交
的直径,AB、AC的延长线分别交 于D、E,过B点作
于D、E,过B点作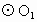 的切线交AE于F.
的切线交AE于F.

求证:BF∥DE.
|
证明:连接 BC.
∵ AB是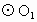 的直径, 的直径,
∴∠ ACB=90°,又四边形 BCED是 的内接四边形, 的内接四边形,
∴∠ BDE+∠BCE=180°∵∠ BCA+∠BCE=180°∴∠ BDE=∠ACB=90°,∵ BF是过点B的 的切线, 的切线,
∴∠ ABF=90°,∴∠ ABF=∠D,∴ BF∥DE. |
|
欲证 BF∥DE,根据平行线的判定,需要利用同位角、内错角、同旁内角,图形中可直接看到同位角,如果能证明∠D=∠ABF,则结论可得,但因这两个角分别在两个圆里,没有相应的定理予以保证,所以怎样把两个圆的角转化到一个圆中,或找个“中介”转换一下,成为解决问题的关键点.此时,连接公共弦,利用“圆内接四边形的外角等于内对角”,即可得结论.当遇到两个相交圆时,如果需要沟通角的关系时,往往需要连接辅助线——公共弦. |


科目:初中数学 来源:素质教育新学案·初中几何·第三册 题型:044
解答题
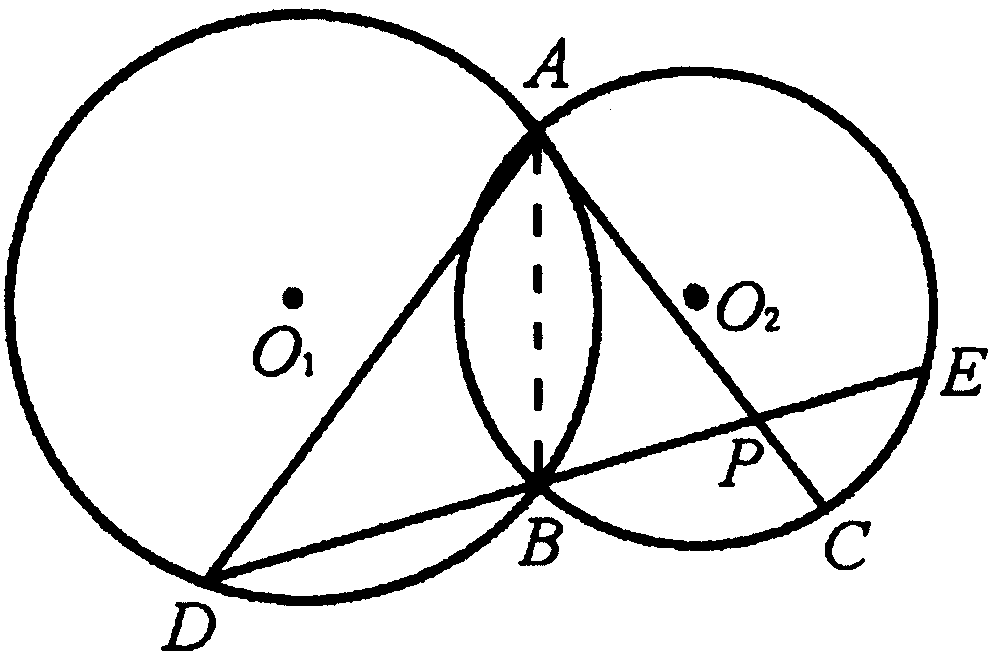
如图所示,已知⊙![]() 与⊙
与⊙![]() 相交于A、B两点,过点A作⊙
相交于A、B两点,过点A作⊙![]() 的切线交⊙
的切线交⊙![]() 于点C,过点B作两圆的割线分别交⊙
于点C,过点B作两圆的割线分别交⊙![]() 、⊙
、⊙![]() 于点D、E,和AC交于点P.
于点D、E,和AC交于点P.
(1)求证PA·PE=PC·PD;
(2)当AD与⊙![]() 相切,且PA=6,PC=2,PD=12时,求AD的长.
相切,且PA=6,PC=2,PD=12时,求AD的长.
查看答案和解析>>
科目:初中数学 来源:素质教育新学案·初中几何·第三册 题型:044
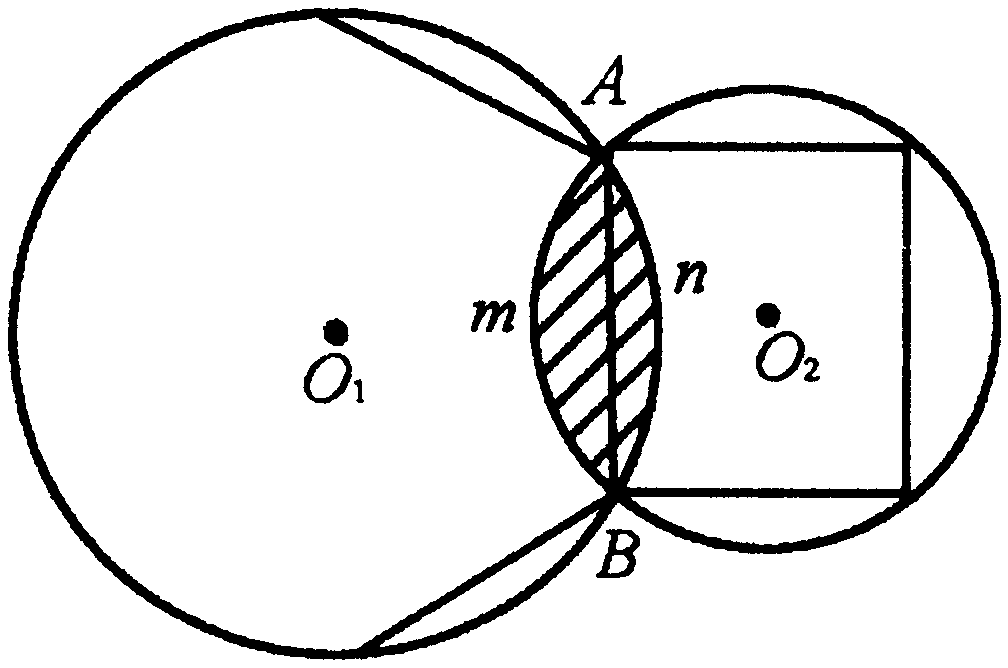
如图所示,已知⊙![]() 与⊙
与⊙![]() 相交于A、B两点,AB=12cm,且AB分别是⊙
相交于A、B两点,AB=12cm,且AB分别是⊙![]() 与⊙
与⊙![]() 内接正六边形和内接正方形的边,求阴影部分面积.
内接正六边形和内接正方形的边,求阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com