
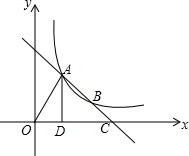
 如图,直线AB交双曲线y=$\frac{k}{x}$于A,B,交x轴于点C,过A作AD⊥x轴于D,且OD=$\frac{1}{3}$OC,S△OAC=12.则k的值为8.
如图,直线AB交双曲线y=$\frac{k}{x}$于A,B,交x轴于点C,过A作AD⊥x轴于D,且OD=$\frac{1}{3}$OC,S△OAC=12.则k的值为8.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
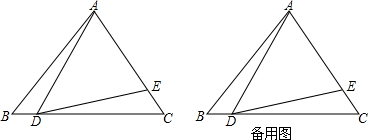
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
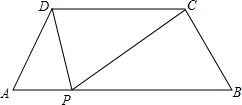 如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.
如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
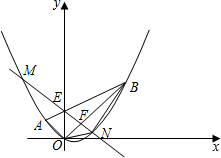 如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.
(1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
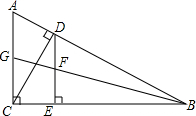 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com