
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.
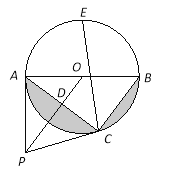
【答案】(1)证明见解析;
(2)阴影部分的面积为![]() ;
;
(3)CE的长是![]()
【解析】(1)连接OC,证明△PAO≌△PCO,得到∠PAO=∠PCO=90 ,证明结论;
(2)证明△ADO∽△PDA,得到成比例线段求出BC的长,根据S阴=S半⊙O-S△ACB求出答案;
(3)连接AE,BE,过点B作BM⊥CE于点M,分别求出CM和EM的长,求和得到答案.
证明: ⑴如图,连接OC,
∵PA切⊙O于A.
∴∠PAO=90.
∵OP∥BC,
∴∠AOP=∠OBC,∠COP=∠OCB.
∵OC=OB,
∴∠OBC=∠OCB,
∴∠AOP=∠COP.
又∵OA=OC,OP=OP,
∴△PAO≌△PCO (SAS).
∴∠PAO=∠PCO=90 ,
又∵OC是⊙O的半径,
∴PC是⊙O的切线.
⑵解法一:
由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90 ,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD =∠AOD,
∴△ADO∽△PDA.
∴![]() ,
,
∴![]() ,
,
∵AC=8, PD=![]() ,
,
∴AD=![]() AC=4,OD=3,AO=5,
AC=4,OD=3,AO=5,
由题意知OD为△ABC的中位线,
∴BC=2OD=6,AB=10.
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
解法二:

∵AB是⊙O的直径,OP∥BC,
∴∠PDC=∠ACB=90.
∵∠PCO=90 ,
∴∠PCD+∠ACO=∠ACO+∠OCB=90 ,
即∠PCD=∠OCB.
又∵∠OBC =∠OCB,
∴∠PCD=∠OBC,
∴△PDC∽△ACB,
∴![]() .
.
又∵AC=8, PD=![]() ,
,
∴AD=DC=4,PC=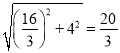 .
.
∴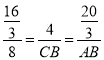 ,
,
∴CB=6,AB=10,
∴S阴=![]() .
.
答:阴影部分的面积为![]() .
.
(3)如图,连接AE,BE,过点B作BM⊥CE于点M.
∴∠CMB=∠EMB=∠AEB=90,
又∵点E是![]() 的中点,
的中点,
∴∠ECB=∠CBM=∠ABE=45,CM=MB =![]() ,BE=ABcos45=
,BE=ABcos45=![]() ,
,
∴ EM=![]() ,
,
∴CE=CM+EM=![]() .
.
“点睛”本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.


科目:初中数学 来源: 题型:
【题目】已知Rt△ABD中,边AB=OB=1,∠ABO=90°
问题探究:
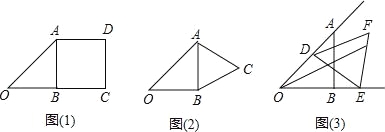
(1)以AB为边,在Rt△ABO的右边作正方形ABC,如图(1),则点O与点D的距离为 .
(2)以AB为边,在Rt△ABO的右边作等边三角形ABC,如图(2),求点O与点C的距离.
问题解决:
(3)若线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图(3),则点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用12000元购进甲、乙两种商品.其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:
倍多15件,甲、乙两种商品的进价和售价如下表:
甲 | 乙 | |
进价(元件) | 44 | 60 |
售价(元件) | 58 | 80 |
(1)该超市第一次购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多360元,求第二次乙商品是按原价打几折销售?(提示:设原价打![]() 折销售,则实际售价=原价
折销售,则实际售价=原价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
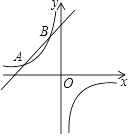
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
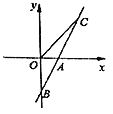
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
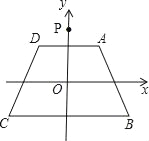
A. (2010,2) B. (2010,﹣2) C. (2012,﹣2) D. (0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
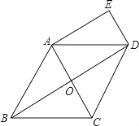
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
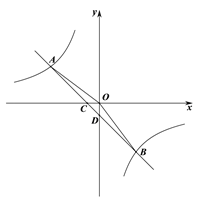
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数图象交于第二,四象限内A,B两点,与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点D.若点B的纵坐标为
轴交于点D.若点B的纵坐标为![]() ,OA=5,
,OA=5, ![]() .
.
(1)求反比例函数解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com