
分析 (1)画树状图展示所有36种等可能的结果数,再找出两个朝上数字的积为偶数的结果数,然后根据概率公式求解;
(2)利用(1)中的结论易得平均每次甲得$\frac{3}{4}$分,平均每次乙得$\frac{1}{4}$分;
(3)利用甲获胜的概率和乙获胜的概率的大小关系进行判断;
(4)可改变等分使游戏公平:如得到的积为偶数则甲得1分,否则乙得3分;也可改变两数的运算方式:如得到的和为偶数则甲获胜,否则乙获胜等等.
解答 解:(1)画树状图为: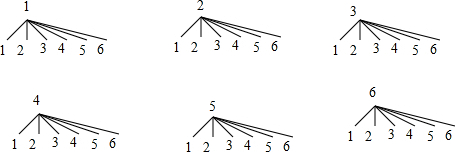
共有36种等可能的结果数,其中两个朝上数字的积为偶数的结果数为27,
所以两个朝上数字的积为偶数的概率=$\frac{27}{36}$=$\frac{3}{4}$;
(2)若得到的积为偶数则甲得1分,否则乙得1分,平均每次甲得$\frac{3}{4}$分,平均每次乙得$\frac{1}{4}$分;
(3)这个游戏对甲、乙双方不公平.因为甲获胜的概率=$\frac{3}{4}$,乙获胜的概率=$\frac{1}{4}$.
(4)规则可改为:若得到的积为偶数则甲得1分,否则乙得3分.
也可改为若得到的和为偶数则甲获胜,否则乙获胜等等.
点评 本题考查了游戏公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.


科目:初中数学 来源: 题型:选择题
 已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )
已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,∠ABC=90°,D为AC中点,将线段DC绕点D旋转,得到线段DE,连接AE,CE;
在△ABC中,∠ABC=90°,D为AC中点,将线段DC绕点D旋转,得到线段DE,连接AE,CE;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 服装厂为了估计某校七年级学生穿不同尺码校服的人数,从该校七年级学生中随机抽取了若干名学生的身高数据(单位:cm),绘制成了频数分布表和频数分布直方图(不完整).
服装厂为了估计某校七年级学生穿不同尺码校服的人数,从该校七年级学生中随机抽取了若干名学生的身高数据(单位:cm),绘制成了频数分布表和频数分布直方图(不完整).| 身高x | 频数 | 百分比 |
| 145≤x<150 | 10 | 20% |
| 150≤x<155 | 11 | 22% |
| 155≤x<160 | m | 30% |
| 160≤x<165 | 7 | n |
| 165≤x<170 | 5 | 10% |
| 170≤x<175 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△CDE的顶点C坐标为(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上,抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A.
如图,在平面直角坐标系中,△CDE的顶点C坐标为(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上,抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com