
分析 (1)因为25<28<30,所以把x=28代入y=40-x即可求出该产品的年销售量为多少万件;
(2)由(1)中y于x的函数关系式和根据年获利=年销售收入-生产成本-投资成本,得到w和x的二次函数关系,再有x的取值范围不同分别讨论即可知道该公司是盈利还是亏损,若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3)由题目的条件得到w和x在自变量x的不同取值范围的函数关系式,再分别当w≥67.5,求出对应x的范围,结合y于x的关系中的x取值范围即可确定此时销售单价的范围.
解答 解:(1)∵25<28<30,y=$\left\{{\begin{array}{l}{40-x(25≤x≤30)}\\{25-0.5x(30<x≤35)}\end{array}}\right.$,
∴把x=28代入y=40-x得,
∴y=12(万件),
答:当销售单价定为28元时,该产品的年销售量为12万件;
(2)①当 25≤x≤30时,W=(40-x)(x-20)-25-100=-x2+60x-925=-(x-30)2-25,
故当x=30时,W最大为-25,即公司最少亏损25万;
②当30<x≤35时,W=(25-0.5x)(x-20)-25-100
=-$\frac{1}{2}$x2+35x-625=-$\frac{1}{2}$(x-35)2-12.5
故当x=35时,W最大为-12.5,即公司最少亏损12.5万;
对比①,②得,投资的第一年,公司亏损,最少亏损是12.5万;
答:投资的第一年,公司亏损,最少亏损是12.5万;
(3)①当 25≤x≤30时,W=(40-x)(x-20-1)-12.5-10=-x2+61x-862.5,
令W=67.5,则-x2+61x-862.5=67.5,
化简得:x2-61x+930=0,
解得:x1=31;x2=30,
此时,当两年的总盈利不低于67.5万元,x=30;
②当30<x≤35时,W=(25-0.5x)(x-20-1)-12.5-10=-0.5x2+35.5x-547.5,
令W=67.5,则-0.5x2+35.5x-547.5=67.5,
化简得:x2-71x+1230=0,
解得:x1=30;x2=41,
此时,当两年的总盈利不低于67.5万元,30<x≤35,
答:到第二年年底,两年的总盈利不低于67.5万元,此时销售单价的范围是30≤x≤35.
点评 本题主要考查二次函数在实际中应用,最大销售利润的问题常利函数的增减性来解答,我们首先要弄懂题意,确定变量,建立函数模型解答,其中要注意应该在自变量的取值范围内求最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
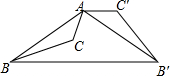 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
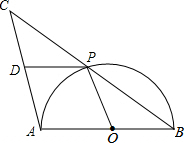 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
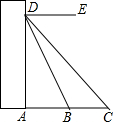 如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)
如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
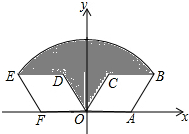 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com