
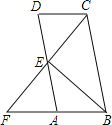
【题目】如图,四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)试说明:CD=AF;
(2)若BC=BF,试说明:BE⊥CF.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由CD∥AB,可得∠CDE=∠FAE,而E是AD中点,因此有DE=AE,再有∠AEF=∠DEC,所以利用ASA可证△CDE≌△FAE,再利用全等三角形的性质,可得CD=AF;
(2)先利用(1)中的三角形的全等,可得CE=FE,再根据BC=BF,利用等腰三角形三线合一的性质,可证BE⊥CF.
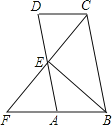
证明:(1)∵CD∥AB,
∴∠CDE=∠FAE,
又∵E是AD中点,
∴DE=AE,
又∵∠AEF=∠DEC,
∴△CDE≌△FAE,
∴CD=AF;
(2)∵BC=BF,
∴△BCF是等腰三角形,
又∵△CDE≌△FAE,
∴CE=FE,
∴BE⊥CF(等腰三角形底边上的中线与底边上的高相互重合).


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教用品商店欲购进![]() 、
、![]() 两种笔记本,用
两种笔记本,用![]() 元购进的
元购进的![]() 种笔记本与用
种笔记本与用![]() 元购进的
元购进的![]() 种笔记本的数量相同,每本
种笔记本的数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵
种笔记本的进价贵![]() 元.
元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店![]() 种笔记本每本售价
种笔记本每本售价![]() 元,
元,![]() 种笔记本每本售价
种笔记本每本售价![]() 元,准备购进
元,准备购进![]() 、
、![]() 两种笔记本共
两种笔记本共![]() 本,且这两种笔记本全部售出后总获利不小于
本,且这两种笔记本全部售出后总获利不小于![]() 元,则最多购进
元,则最多购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am![]() +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y
+bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y![]() )在该抛物线上,则y>y
)在该抛物线上,则y>y![]() .其中正确的结论有___________ .(写出所有正确结论的序号)
.其中正确的结论有___________ .(写出所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
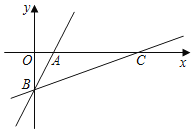
【题目】如图,在平面直角坐标系中,一次函数y=2x﹣4的图象分別交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
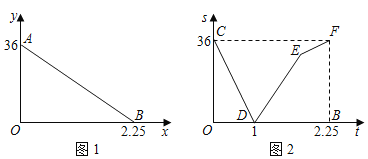
【题目】小明从家出发沿一条笔直的公路骑自行车前往图书馆看书,他与图书馆之间的距离y(km)与出发时间t(h)之间的函数关系如图1中线段AB所示,在小明出发的同时,小明的妈妈从图书馆借书结束,沿同一条公路骑电动车匀速回家,两人之间的距离s(km)与出发时间t(h)之间的函数关系式如图2中折线段CD﹣DE﹣EF所示.
(1)小明骑自行车的速度为 km/h、妈妈骑电动车的速度为 km/h;
(2)解释图中点E的实际意义,并求出点E的坐标;
(3)求当t为多少时,两车之间的距离为18km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 小明遇到这样一个问题
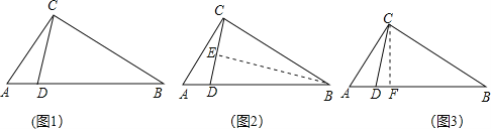
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
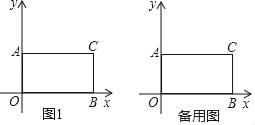
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到△D'CB'(点D'与点D对应).
①若OD=3,求点D'的坐标.
②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com