
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

【答案】(1)证明见解析;(2)菱形.
【解析】试题分析:
(1)这两个三角形有一条直角边相等,一个直角相等只需证还有一条边相等即可;
(2)先证AF是BG的垂直平分线,再分别求出∠BEF和∠BFE的度数.
试题解析:
(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠AOE=∠BOG=90°.
∵BH⊥AF,∴∠AHG=∠AHB=90°,∴∠GAH+∠AGH=90°=∠OBG+∠AGH,
∴∠GAH=∠OBG,即∠OAE=∠OBG.
∴在△OAE与△OBG中, ,
,
∴△OAE≌△OBG(ASA);
(2)解:四边形BFGE为菱形;理由如下:
在△AHG与△AHB中, ,
,
∴△AHG≌△AHB(ASA),∴GH=BH,
∴AF是线段BG的垂直平分线,∴EG=EB,FG=FB.
∵∠BEF=∠BAE+∠ABE=67.5°,∠BFE=90°﹣∠BAF=67.5°,
∴∠BEF=∠BFE,∴EB=FB,∴EG=EB=FB=FG,
∴四边形BFGE是菱形.
点睛;本题主要考查了正方形的性质、三角形全等的判定与性质、菱形的判定、线段垂直平分线的性质等知识点是一个比较难的四边形的综合题,在证明的过程中要注意一个基本几何图形“8字形”的运用,如下图通常称为“8字形”,如果∠A=∠B,那么∠D=∠C,这种寻找角的关系的图形在几何证明中会经常遇到,需要熟悉掌握.



科目:初中数学 来源: 题型:
【题目】解答下列各题
(1)化简并求值:-(3a2-4ab)+[a2-![]() (a+2ab)] ,其中a=-2,b=1
(a+2ab)] ,其中a=-2,b=1
(2)已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度. (结果保留整数,参考数据:sin35°≈ ![]() ,cos35°≈
,cos35°≈ ![]() ,tan35°≈
,tan35°≈ ![]() ,
, ![]() ≈1.7)
≈1.7)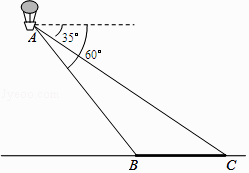
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB. 
(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6 ![]() , ①求图中阴影部分的面积;
, ①求图中阴影部分的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
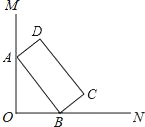
A. ![]() +1 B.
+1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | |
B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com