
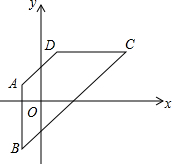
 如图所示,四边形ABCD的四个顶点A、B、C、D的坐标分别为(-1,1)、(-1,-3)、(5,3)、(1,3),则其对称轴的函数表达式为y=-x+2.
如图所示,四边形ABCD的四个顶点A、B、C、D的坐标分别为(-1,1)、(-1,-3)、(5,3)、(1,3),则其对称轴的函数表达式为y=-x+2. 分析 先求出AD、BC的中点坐标,然后设对称轴的函数表达式为y=kx+b(k≠0),利用待定系数法求一次函数解析式解答.
解答 解:易得其对称轴为经过AD、BC的中点的直线,
∵A、B、C、D的坐标分别为(-1,1)、(-1,-3)、(5,3)、(1,3),
∴AD、BC的中点坐标分别为(0,2),(2,0),
设对称轴的函数表达式为y=kx+b(k≠0),
则$\left\{\begin{array}{l}{b=2}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
所以,对称轴的函数表达式为y=-x+2.
故答案为:y=-x+2.
点评 本题考查了待定系数法求一次函数解析式,轴对称的性质,观察图形以及点的坐标确定出对称轴的位置以及对称轴经过的两个点的坐标是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
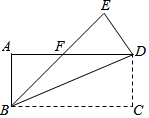 如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.
如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
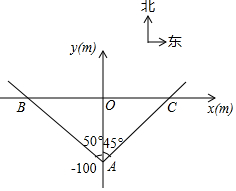 某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
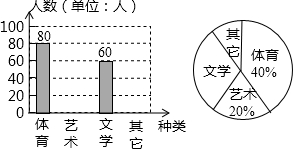 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
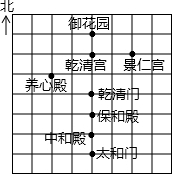 如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2).
如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com