
【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
【答案】(1)平均每分钟一道侧门可以通过80名学生,一道正门可以通过120名学生;(2)符合安全规定
【解析】
(1)我们可设平均每分钟一道侧门可以通过x名学生,则一道正门可以通过(x+40)名学生,根据题意列方程解答即可.
(2)我们先求出这栋楼最多有学生,再求出拥挤时5分钟3道门能通过多少名学生,比较后即可得出结论.
解:(1)设平均每分钟一道侧门可以通过x名学生,则一道正门可以通过(x+40)名学生,
根据题意列方程:2x+2(x+40)=400
解这个方程得:x=80
∴x+40=120
答:平均每分钟一道侧门可以通过80名学生,则一道正门可以通过120名学生.
(2)这栋楼最多有学生4×6×45=1080(人)
拥挤时5分钟3道门能通过![]() (人)
(人)
1280>1080
建造的3道门符合安全规定.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)中,对任意相邻的上下或左右两格中的数字同时加1或减2,这算作一次操作,经过若干次操作后,图(1)能变为图(2),则图(2)中A格内的数是_____
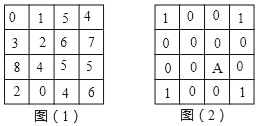
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A—C—B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1 , C2两段组成,如图2所示.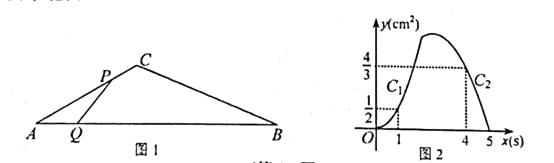
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
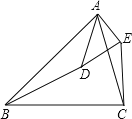
【题目】如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)求证:△ABC∽△ADE;
(2)判断△ABD与△ACE是否相似?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC. 
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可). 
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. 
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求∠OCA度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com