
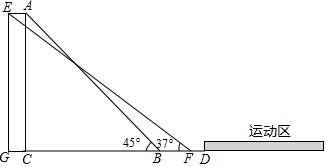
分析 在Rt△ABC中通过解直角三角形可求出BC的长度,在Rt△EFG中通过解直角三角形可求出GF的长度,由EG=AC=15m、AC⊥BC、EG⊥BC可得出四边形EGCA是矩形,进而可得出GC的长度,再根据BF=GF-GC-BC、FD=BD-BF即可求出FD的长度,由FD的长度小于2.5米可得出施工方提供的设计方案不满足安全要求.
解答 解:施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC=$\frac{AC}{tan45°}$=15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=$\frac{EG}{tan37°}$≈$\frac{15}{\frac{3}{4}}$=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴BF=GF-GC-BC≈20-15-2=3m.
∵BD=5m,
∴FD=BD-BF≈5-3=2<2.5,
∴施工方提供的设计方案不满足安全要求.
点评 本题考查了解直角三角形的应用中的坡度坡角问题,通过解直角三角形求出BC、GF的长度是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -19 | B. | -15 | C. | -13 | D. | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
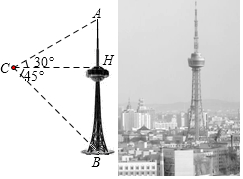 吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)
吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com