
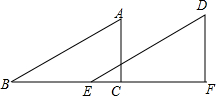
 如图,把三角形△ABC沿直线BC的方向平移6cm得到三角形DEF,已知∠A=63°,∠B=27°,AC=4cm,BC=8cm,你能求出哪些角的度数?哪些边的长度?请直接写出结果.(至少写出5个结果)
如图,把三角形△ABC沿直线BC的方向平移6cm得到三角形DEF,已知∠A=63°,∠B=27°,AC=4cm,BC=8cm,你能求出哪些角的度数?哪些边的长度?请直接写出结果.(至少写出5个结果) 分析 利用三角形内角和可计算出∠ACB=90°,则利用勾股定理可计算出AB=4$\sqrt{5}$cm,然后根据平移的性质得到△DEF各边的长和各内角的度数,同时得到BE=CF=6cm,EC=2cm.
解答 解:∵∠A=63°,∠B=27°,
∴∠ACB=180°-63°-27°=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$cm,
∵三角形△ABC沿直线BC的方向平移6cm得到三角形DEF,
∴∠DEF=∠B=27°,∠D=∠A=63°,∠F=∠ACB=90°,DF=AC=4cm,EF=BC=8cm,DE=AB=4$\sqrt{5}$cm,BE=CF=6cm,EC=2cm.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.


科目:初中数学 来源: 题型:选择题
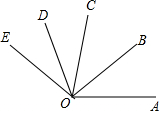 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )| A. | 50° | B. | 62° | C. | 69° | D. | 76° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com