
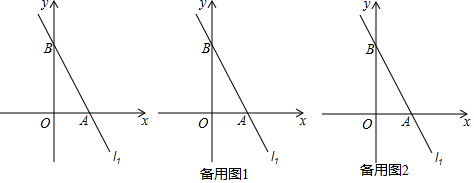
���� ���A��B��������꣬�����C�����꣬���ô���ϵ�������ɵó�ֱ��B��C�Ľ���ʽ��
��1���ֱ����A��B������������ֱ��y=x�ĶԳƵ㣬�����ô���ϵ������������ʽ���ɣ�
��2����M����ֱ��l4��l1��l4��y���ڵ�D����MN��y���ڵ�N�����MN��BN�ij�����ND=a����MN=$\frac{1}{2}$��BN=1��BD=a+1�����ݹ��ɶ������a��ֵ�����ô���ϵ�������ֱ��l4�ı���ʽ���ɣ�
���  �⣺��ͼ1����ֱ��l1�ı���ʽΪy=-2x+6��
�⣺��ͼ1����ֱ��l1�ı���ʽΪy=-2x+6��
��ֱ��l1��x��Ľ���A������Ϊ��3��0������y��Ľ���B������Ϊ��0��6����
���A����y��ĶԳƵ�C������Ϊ��-3��0����
��ֱ��BC�Ľ���ʽΪy=kx+b��k��0����
��$\left\{\begin{array}{l}{b=6}\\{-3k+b=0}\end{array}\right.$��
���k=2��
��ֱ��l2�ı���ʽΪ��y=2x+6��
�ʴ�Ϊ��y=2x+6��
��1����ͼ2����A��3��0����B��0��6����
��A��B������������ֱ��y=x�ĶԳƵ�ֱ�ΪA�䣨0��3����B�䣨6��0����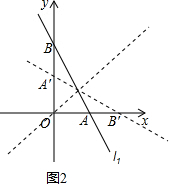
��ֱ��A��B��Ľ���ʽΪy=ax+c��
��$\left\{\begin{array}{l}{c=3}\\{6a+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=3}\end{array}\right.$��
��ֱ��l2�ı���ʽΪ��y=-$\frac{1}{2}$x+3��
��2����ͼ3����M����ֱ��lA��l1��lA��y���ڵ�D����MN��y���ڵ�N��
�ߵ�M��m��4����ֱ��l1�ϣ�
��-2m+6=4��
��m=1��
��MN=1��BN=2��
��BM=$\sqrt{5}$��
��ND=a����MN=1��BN=2��BD=a+2��
�ɹ��ɶ����ã���a+2��2=a2+12+��$\sqrt{5}$��2��
��ã�a=$\frac{1}{2}$
��D��0��$\frac{7}{2}$����
��ֱ��lA�ı���ʽy=kx+$\frac{7}{2}$��
��M��1��4������ã�k=$\frac{1}{2}$
��ֱ��lA�ı���ʽy=$\frac{1}{2}$x+$\frac{7}{2}$��
���� ���⿼����һ�κ����ۺ��⣬��Ҫ����һ�κ�����ͼ���뼸�α任���������⻭������ͼ�����ô���ϵ��������ǽ�����Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
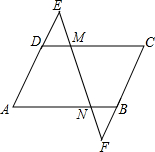 ��ͼ��ֱ��EF�ֱ�CD��AB��M��N����EMD=65�㣬��MNB=115�㣬�ҡ�EDM=��FBN�������н�����ȷ���У�������
��ͼ��ֱ��EF�ֱ�CD��AB��M��N����EMD=65�㣬��MNB=115�㣬�ҡ�EDM=��FBN�������н�����ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
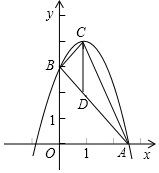 ��ͼ��������y=-x2+2x+3��������Ϊ��C����x���������ڵ�A����y���ڵ�B����P�������ߣ��ڵ�һ�����ڣ��ϵ�һ�����㣬����PA��PB��
��ͼ��������y=-x2+2x+3��������Ϊ��C����x���������ڵ�A����y���ڵ�B����P�������ߣ��ڵ�һ�����ڣ��ϵ�һ�����㣬����PA��PB���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com