
【题目】甲、乙两人以各自的交通工具、相同路线,前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②乙走了8km后遇到甲;③乙出发6分钟后追上甲;④甲走了28分钟时,甲乙相距3km.其中正确的是( )

A. 只有① B. ①③ C. ②③④ D. ①③④
科目:初中数学 来源: 题型:
【题目】将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( ) 
A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.都不相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0)…… 根据这个规律探索可得,第50个点的坐标为( )
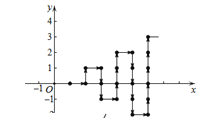
A. (10,-5)B. (10,-1) C. (10,0) D. (10,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D是AB边上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.
(1)求证:CD=DE;

(2)若D是AB延长线上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.请画出图形,判断CD=DE是否还成立?若成立,请给予证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系.经测量,在海拔高度为1000米的地方,空气含氧量约为267克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)求出海拔高度为0米的地方的空气含氧量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.

(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com