
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
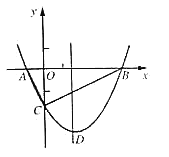
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
【答案】(1)![]() ,D
,D![]() ;(2)
;(2)![]() 是直角三角形,见解析;(3)
是直角三角形,见解析;(3)![]() ,
,![]() .
.
【解析】
(1)直接将(1,0),代入解析式进而得出答案,再利用配方法求出函数顶点坐标;
(2)分别求出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,进而利用勾股定理的逆定理得出即可;
(3)利用轴对称最短路线求法得出M点位置,求出直线![]() 的解析式,可得M点坐标,然后易求此时△ACM的周长.
的解析式,可得M点坐标,然后易求此时△ACM的周长.
解:(1)∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() .
.
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴顶点![]() 的坐标为:
的坐标为:![]() ;
;
(2)![]() 是直角三角形,
是直角三角形,
证明:当![]() 时
时![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形;
是直角三角形;
(3)如图所示:BC与对称轴交于点M,连接![]() ,
,
根据轴对称性及两点之间线段最短可知,此时![]() 的值最小,即
的值最小,即![]() 周长最小,
周长最小,
设直线![]() 解析式为:
解析式为:![]() ,则
,则![]() ,
,
解得: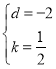 ,
,
故直线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线对称轴为![]()
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
![]() 最小周长是:
最小周长是:![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
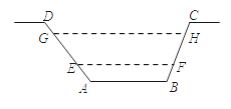
A. 1.2 B. 1.1 C. 0.8 D. 2.2
查看答案和解析>>
科目:初中数学 来源: 题型:
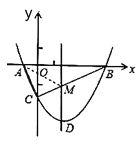
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
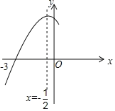
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 为方程
为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
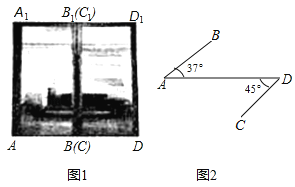
【题目】图1是一商场的推拉门,已知门的宽度![]() 米,且两扇门的大小相同(即
米,且两扇门的大小相同(即![]() ),将左边的门
),将左边的门![]() 绕门轴
绕门轴![]() 向里面旋转
向里面旋转![]() ,将右边的门
,将右边的门![]() 绕门轴
绕门轴![]() 向外面旋转
向外面旋转![]() ,其示意图如图2,求此时
,其示意图如图2,求此时![]() 与
与![]() 之间的距离(结果保留一位小数).(参考数据:
之间的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扫地机器人能够自主移动并作出反应,是因为它发射红外信号反射回接收器,机器人在打扫房间时,若碰到障碍物则发起警报.若某一房间内A、B两点之间有障碍物,现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(6,4),机器人沿抛物线y=ax2﹣4ax﹣5a运动.若机器人在运动过程中只触发一次报警,则a的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
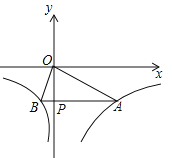
【题目】(2017四川省达州市,第10题,3分)已知函数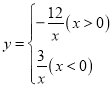 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(![]() ,
,![]() ).
).
其中正确的结论个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
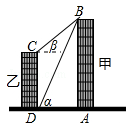
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次活动共调查了多少人;
(2)将条形统计图补充完整;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com