练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一勘测人员从B点出发，沿坡角为15°的坡面以5千米/时的速度行至D处，用了12分钟，然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处，用了10分钟，求山高（即AC的长度）及（即BC的长）（精确到0.01千米）．

    【答案】1.44千米

    【解析】

    试题过D作DF⊥BC于F，先求得BD、AD的长，再在Rt△BFD中，根据正弦函数求得DF、BF的长，在Rt△ADE中，根据余弦函数求得DE、AE的长，即可求得结果.

    过D作DF⊥BC于F

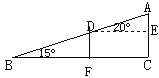
    由已知得BD=5×=1(千米)，AD=3×=0.5(千米)

    在Rt△BFD中，DF=BD·sin15°≈0.2588(千米)

    BF=BD·cos15°≈0.9659(千米)

    在Rt△ADE中，DE=AD·cos20°≈0.4698(千米)

    AE=AD·sin20°≈0.1710(千米)

    故AC=AE+EC=AE+DF=0.1710+0.2588=0.4298≈0.43(千米)

    BC=BF+CF=BF+DE=0.9659+0.4698=1.4357≈1.44(千米).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=x2﹣（m+1）x+m

    （1）求证：抛物线与x轴一定有交点；

    （2）若抛物线与x轴交于A（x1，0），B（x2，0）两点，x1＜0＜x2，且，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

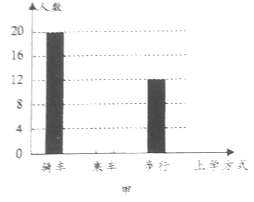
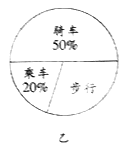
    【题目】学习了统计知识后，数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计．如图甲乙是数学兴趣小组的同学们通过手机和整理数据后，绘制的两幅不完整的统计图．

    请你根据图中提供的信息，解答一下的问题：

    （1）在扇形统计图中，计算出“步行”部分所应对的圆心角的度数．

    （2）请问该班共有多少名学生？

    （3）在图中将表示“乘车”的部分补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“新中梁山隧道”于2017年11月21日开放通行，原中梁山隧道将封闭升级，扩容改造工程预计2018年3月全部完工，届时将实现双向8车道通行，隧道通行能力将增加一倍，沿线交通拥堵状况将有所缓解．图中线段AB表示该工程的部分隧道．无人勘测机从隧道侧的A点出发时，测得C点正上方的E点的仰角为45°，无人机飞行到E点后，沿着坡度i=1：3的路线EB飞行，飞行到D点正上方的F点时，测得A点的俯角为12°，其中EC=100米，A、B、C、D、E、F在同一平面内，则隧道AD段的长度约为（　　）米，（参考数据：tan12°≈0.2，cosl2°≈0.98）

    A. 200 B. 250 C. 300 D. 540

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算或化简：

    （1）sin45°cos60°﹣cos45°sin30°；

    （2）5tan30°﹣2（cos60°﹣sin60°）；

    （3）（tan30°）2005（2sin45°）2004；

    （4）（2cos45°﹣tan45°）﹣（tan60°+sin30°）0﹣（2sin45°﹣1）﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题背景：如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E，F分别是BC，CD上的点，且∠EAF＝60°，请探究图中线段BE，EF，FD之间的数量关系是什么？

    小明探究此问题的方法是：延长FD到点G，使DG＝BE，连结AG．先证明△ABE≌△ADG，得AE＝AG；再由条件可得∠EAF＝∠GAF，证明△AEF≌△AGF，进而可得线段BE，EF，FD之间的数量关系是　 　．

    （2）拓展应用：

    如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E，F分别是BC，CD上的点，且∠EAF＝∠BAD．问（1）中的线段BE，EF，FD之间的数量关系是否还成立？若成立，请给出证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：

    ①∠CAD=30°②BD=③S平行四边形ABCD=ABAC④OE=AD⑤S△APO=，正确的个数是（　　）

    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把一张长，宽的矩形硬纸板的四周各剪去一个同样大小的小正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．设剪去的小正方形的边长为．

    请用含的代数式表示长方体盒子的底面积；

    当剪去的小正方形的边长为多少时，其底面积是？

    试判断折合而成的长方体盒子的侧面积是否有最大值？若有，试求出最大值和此时剪去的小正方形的边长；若没有，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】实验探究：下面设想用电脑模拟台球游戏，为简单起见，约定：①每个球或球袋都视为一点，如不遇障碍，各球均沿直线前进；②A球击中B球，意味着B球在A球前进的路线上，且B球被撞击后沿着A球原来的方向前进；③球撞及桌边后的反弹角等于入射角（即∠α＝∠β）．如图，设桌面上只剩下白球A和6号球B，希望A球撞击桌边上C点后反弹，再击中B球．

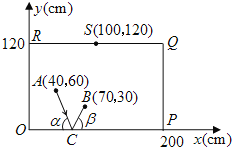
    （1）在桌面上建立如图所示的坐标系，白球A（40，60）和6号球B（70，30），利用一次函数的知识，求出C点坐标；

    （2）设桌边RQ上有球袋S（100，120），判定6号球被从C点反弹出的白球撞击后，能否落入球袋S中（假定6号球被撞击后的速度足够大），并说明理由．

    查看答案和解析>>

    同步练习册答案