
【题目】如图,∠ XOY=900,OW平分∠XOY,PA⊥OX,PB ⊥OY,PC⊥OW.若OA+ OB+OC=1,则OC=( ).

A. 2-![]() B.
B. ![]() -1 C.
-1 C. ![]() -2 D. 2
-2 D. 2![]() -3
-3
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),且与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)点P是y轴正半轴上的一个动点,连结DP,将线段DP绕着点D顺时针旋转90°得到线段DE,点P的对应点E恰好落在抛物线上,求出此时点P的坐标;
(3)点M(m,n)是抛物线上的一个动点,连接MD,把MD2表示成自变量n的函数,并求出MD2取得最小值时点M的坐标.
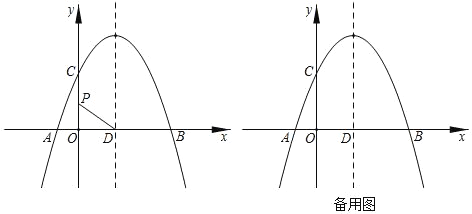
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数m、n,定义一种运算“※”为:m※n=mn+n.
(1)求2※5与2※(﹣5)的值;
(2)如果关于x的方程x※(a※x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数;
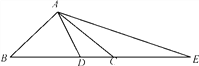
(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内,直线y=-x+5与![]() 轴和
轴和![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
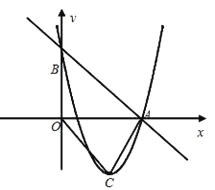
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为![]() .
.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com