Question

18．如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C，D．延长BO交PA的延长线于点F．若⊙O的半径为r，△PCD的周长等于3r．
（1）求PA的长（用r表示）；
（2）求tan∠APB的值．

Answer 1

分析 （1）根据切线长定理易得PA=PB，CA=CE，DE=DB，再由△PCD的周长等于3r，即可求出PA的长；
（2）连接OA，首先证明△FAO∽△FBP，由相似三角形的性质可得$\frac{AO}{BP}=\frac{AF}{BF}$，设AF=x，OF=y，则$\frac{r}{\frac{3}{2}r}=\frac{x}{r+y}$①，再在Rt△AFO中，AF²=OA²+OF²②，由①②可得x和r的关系，进而可求出tan∠APB的值．

解答 解：（1）∵PA，PB切⊙O于A，B两点，CD切⊙O于点E，
∴PA=PB，CA=CE，DE=DB，
∴△PCD的周长=PA+PB=2PA=3r，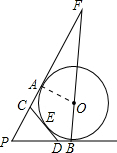
∴PA=$\frac{3}{2}$r；

（2）连接AO，
∵PA，PB切⊙O于A，B两点，
∴∠OAF=∠FBP=90°，
∴∠F+∠P=90°，∠F+∠AOF=90°，
∴∠APB=∠AOF，
∴△FAO∽△FBP，
∴$\frac{AO}{BP}=\frac{AF}{BF}$，
设AF=x，OF=y，
∴$\frac{r}{\frac{3}{2}r}=\frac{x}{r+y}$①，
在Rt△AFO中，AF²=OA²+OF²，
即y²=x²+r²②，
∴x=$\frac{12}{5}$r，
∴tan∠APB=tan∠AOF=$\frac{AF}{AO}$=$\frac{12}{5}$．

点评 本题考查了切线的性质、切线长定理、相似三角形的判定和性质、勾股定理的运用以及锐角三角函数的定义，解题的关键是求tan∠APB的值转化为求tan∠AOF的值，题目的难度不小．