
【题目】如图,AB是△ABC外接圆⊙O的直径,D是AB延长线上一点,且BD= ![]() AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、EF.
AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、EF.
(1)求证:CD是⊙O的切线;
(2)求:tan∠BFE的值.
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=30°,
∴BC= ![]() ,
,
∵OB= ![]() ,BD=
,BD= ![]() ,
,
∴BC=OB=BD,
∴BC= ![]() ,
,
∴OC⊥CD,
∵OC是半径,
∴CD是⊙O的切线;
(2)解:过点E作EH⊥BF于H, 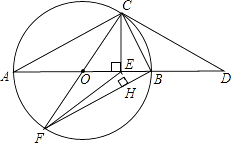
设EH=a,
∵CF是⊙O直径,
∴∠CBF=90°=∠ACB,
∴∠CBF+∠ACB=180°,
∴AC∥BF,
∴∠ABF=∠A=30°,
∴BH= ![]() EH=a
EH=a ![]() ,BE=2EH=2a,
,BE=2EH=2a,
∵CE⊥AB于E,
∴∠A+∠ABC=90°=∠ECB+∠ABC,
∴∠ECB=∠A=30°,
∴BC=2BE=4a,
∵∠BFC=∠A=30°,∠CBF=90°,
∴BF= ![]() =4a
=4a ![]() ,
,
∴FH=BF﹣BH=4a ![]() ﹣a
﹣a ![]() =3a
=3a ![]() ,
,
∴tan∠BFE= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据已知条件证得OC⊥CD,再有切线的判定即可得到CD是⊙O的切线;
(2)过点E作EH⊥BF于H,设EH=a,利用角之间的关系可得到AC∥BF,从而得到BH和BE的长,进而可得到BF的长,此时可求得FH的长,即可求得所求结答案.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,OC=CB=4.
(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等.若存在,求点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2= ![]() AFGF;
AFGF;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1: ![]() .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次艺术作品制作比赛中,某小组八件作品的成绩![]() 单位:分
单位:分![]() 分别是:7、9、8、9、8、10、9、7,下列说法不正确的是
分别是:7、9、8、9、8、10、9、7,下列说法不正确的是![]()
![]()
A. 中位数是![]() B. 平均数是
B. 平均数是![]() C. 众数是9D. 极差是3
C. 众数是9D. 极差是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】

(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com