
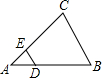
 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为8.
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为8. 分析 由DE∥BC,推出△ADE∽△ABC,可得$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{1}{3}$)2,由S△ADE=1,可得S△ABC=9,由此即可解决问题.
解答 解: ∵DE∥BC,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{1}{3}$)2,
∵S△ADE=1,
∴S△ABC=9,
∴S四边形DBCE=S△ABC-S△ADE=8,
故答案为8.
点评 本题考查相似三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为40°或100°或70°.
如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为40°或100°或70°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某中学课外兴趣活动小组准备围建一个面积为72平方米的矩形苗圃园,其中一边靠18米的墙,另外三边是周长为30米的篱笆围成,则这个苗圃园垂直于墙的一边长为3或12米.
如图,某中学课外兴趣活动小组准备围建一个面积为72平方米的矩形苗圃园,其中一边靠18米的墙,另外三边是周长为30米的篱笆围成,则这个苗圃园垂直于墙的一边长为3或12米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com