
 已知抛物线y=x2-2x-a.
已知抛物线y=x2-2x-a.分析 (1)根据抛物线与x轴有两个交点,△>0即可解题;
(2)当x2-2x-1=0时,求x的值,即可解题;
(3)易求得直线AB的解析式,即可求得点C坐标,根据轴对称可得点D坐标,根据点D在抛物线上即可求得a的值,即可解题.
解答 解:(1)∵抛物线与x轴有两个交点,△>0,∴4+4a>0,a>-1;
(2)代数式x2-2x-1=0时,x=(1-$\sqrt{2}$)或(1+$\sqrt{2}$),
∵介于(1-$\sqrt{2}$)和(1+$\sqrt{2}$)的整数有-1、0、1、2,
∴x的值为-1、0、1、2;
(3)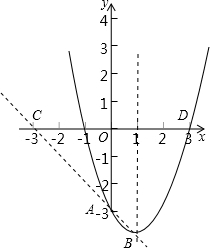
∵抛物线解析式为y=x2-2x-a,
∴对称轴为x=-$\frac{-2}{2}$=1,
∴顶点坐标为(1,-a-1),
∵x=0时,y=-a,
∴点A坐标为(0,-a),
设直线AB解析式为y=kx+b,代入A、B点得:k=-1,b=-a,
∴直线AB解析式为y=-x-a,
∴点C坐标为(-a,0),
∵C,D两点关于y轴对称,
∴点D坐标为(a,0),
∵点D在抛物线上,代入点D得:a2-2a-a=0,解得:a=3,
∵a>-1,∴a=3符合题意,
∴此时a的值为3.
点评 本题考查了代入法求一次函数解析式的方法,考查了抛物线对称轴、顶点的计算,本题中根据点D在抛物线上求得a的值是解题的关键.


科目:初中数学 来源: 题型:解答题
 2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
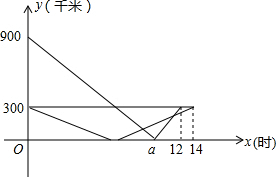 甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
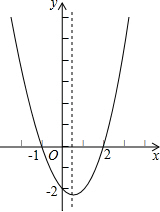 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y<0 | D. | 当x>$\frac{1}{3}$时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
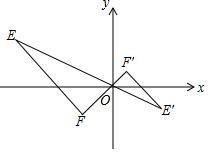 如图,已知E′(2,-1),F′($\frac{1}{2}$,$\frac{1}{2}$),以原点O为位似中心,按比例尺1:2把△EFO扩大,则E′点对应点E的坐标为( )
如图,已知E′(2,-1),F′($\frac{1}{2}$,$\frac{1}{2}$),以原点O为位似中心,按比例尺1:2把△EFO扩大,则E′点对应点E的坐标为( )| A. | (-4,2) | B. | (4,-2) | C. | (-1,-1) | D. | (-1,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com