
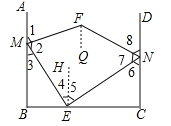
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )

A. 120° B. 135° C. 150° D. 不能确定
【答案】B
【解析】
过F作FQ∥AB,过E作EH∥AB,求出AB∥CD∥EH∥FQ,根据平行线的性质求出∠MFN=∠1+∠8,∠MEN=∠3+∠6=90°,即可求出答案.
∵AB⊥BC,DC⊥BC,∴∠B=∠C=90°,∴∠B+∠C=180°,∴AB∥CD.
∵EM⊥EN,∴∠MEN=90°.
∵MF平分∠AME,NF平分∠DNE,∴∠1=∠2,∠7=∠8.
过F作FQ∥AB,过E作EH∥AB.
∵AB∥CD,∴AB∥CD∥EH,AB∥CD∥FQ,∴∠3=∠4,∠5=∠6,∠1=∠MFQ,∠8=∠NFQ,∴∠MEN=∠4+∠5=∠3+∠6=90°,∠MFN=∠1+∠8.
∵∠1+∠2=180°﹣∠3,∠7+∠8=180°﹣∠6,∴2∠1+2∠8=180°+180°﹣(∠3+∠6)=360°﹣90°=270°,∴∠1+∠8=135°,∴∠MFN=135°.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB =5,AC =4,则△ADF周长为( ).

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
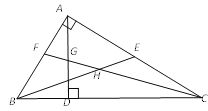
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是
A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
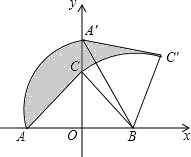
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.

(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com