
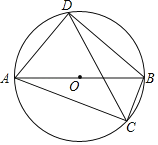
【题目】如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
(1)求AD的长度和四边形ACBD的面积;
(2)证明:2AD2=AC2+BC2.
【答案】(1)AD=3![]() ,四边形ACBD的面积为9+4
,四边形ACBD的面积为9+4![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据圆周角定理得到∠ACB=∠ACD=90°,根据∠ACB的平分线可得![]() ,进而可得AD=BD,再根据勾股定理即可求出AD、AC的长,根据三角形的面积公式计算即可求得四边形ACBD的面积;
,进而可得AD=BD,再根据勾股定理即可求出AD、AC的长,根据三角形的面积公式计算即可求得四边形ACBD的面积;
(2)根据(1)可知AD=BD,根据勾股定理即可得证.
解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
∵∠ACB的平分线交⊙O于D,
∴![]() ,
,
∴AD=BD,
∵在Rt△ABC中,AD2+BD2=AB2,
∴AD=BD=![]() ×AB=3
×AB=3![]() ,
,
∵在Rt△ABC中,AC=![]() ,
,
∴四边形ACBD的面积=![]() ×AD×BD+
×AD×BD+![]() ×BC×AC=9+4
×BC×AC=9+4![]() ;
;
(2)∵∠ACB=∠ACD=90°,
∴AD2+BD2=AB2,AC2+BC2=AB2,
∴AD2+BD2=AC2+BC2,
又∵AD=BD,
∴2AD2=AC2+BC2.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F.
(1)求证:DF是⊙O的切线;
(2)过点F作FG⊥AB,垂足为G,若AB=12.
①求FG的长;
②求点D到FG的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
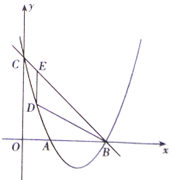
【题目】如图,一次函数![]() 的图象与抛物线
的图象与抛物线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线交
点,抛物线交![]() 轴的另一个交点为点
轴的另一个交点为点![]() (点
(点![]() 的左边).点
的左边).点![]() 为抛物线上一个动点(且点
为抛物线上一个动点(且点![]() 的横坐标
的横坐标![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
(1)求该抛物线的解析式;
(2)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)在(2)的结论下,点![]() 为抛物线上任意一个动点,点
为抛物线上任意一个动点,点![]() 为
为![]() 轴上一个动点,则以
轴上一个动点,则以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形能否为平行四边形,若能,请直接写出点
四点为顶点的四边形能否为平行四边形,若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,有以下四个结论:①ab<0,②b<![]() ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
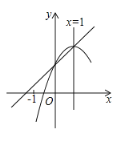
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
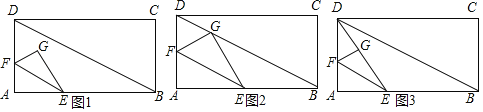
(1)如图2,当EF∥BD,且点G落在对角线BD上时,求DG的长;
(2)如图3,连接DG,当EF∥BD且△DFG是直角三角形时,求AE的值;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出AE的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′ E处,AD′ 与CE交于点F,若∠B=55°,∠DAE=20°,则∠FED′ 的大小为( )
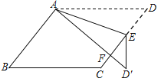
A.20°B.30°
C.35°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案:无纺布的价格均为每吨1.95万元![]() ;
;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨) | 10 | 20 | 35 | … |
A公司花费(万元) | 39 | … | ||
B公司花费(万元) | 40 | … |
(Ⅱ) 设在A公司花费![]() 万元,在B公司花费
万元,在B公司花费![]() 万元,分别求
万元,分别求![]() 、
、![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
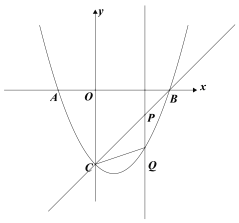
【题目】如图,抛物线y=![]() x2+mx+4m与x轴交于点A(
x2+mx+4m与x轴交于点A(![]() ,0)和点B(
,0)和点B(![]() ,0),与y轴交于点C,
,0),与y轴交于点C,![]() ,若对称轴在y轴的右侧.
,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com