
| 1 | 2 |
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源:解题升级 七年级数学 题型:044
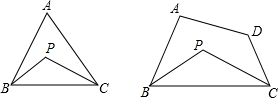
如图所示,(1)P是△ABC内任意一点,求证:AB+AC>BP+CP.
(2)通过上述的证明,你能否受到启发?若在△ABC内有任两点P、Q,连BP、PQ、QC(如图所示),那么AB+AC和BP+PQ+QC的大小关系如何呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源:走向清华北大·初二数学 题型:047
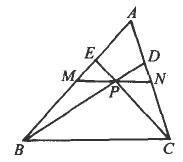
如图,在△ABC中,M、N分别是AB、AC的中点,P是MN上的任一点,BP、CP的延长线分别交AC、AB于D、E.求证:![]() +
+![]() 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com