
| 2 |

| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 知C(0,10),
知C(0,10), 点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t
点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t (s)的函数图像.
(s)的函数图像.

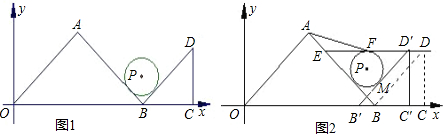
 ⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).
⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).查看答案和解析>>
科目:初中数学 来源:2011年江苏省泰兴市实验初级中学九年级第一次模拟考试数学卷 题型:解答题
(本题12分)如图①,平面直角坐标系中,已 知C(0,10),
知C(0,10), 点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t
点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t (s)的函数图像.
(s)的函数图像.
【小题1】⑴请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图像.
【小题2】⑵求出P、Q两点第一次相遇的时刻.
【小题3】
 ⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).
⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年湖北省天门市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com