
【题目】如图,![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 在直线
在直线![]() 上,若
上,若![]() 是轴对称图形,则
是轴对称图形,则![]() 的度数为__________
的度数为__________
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.
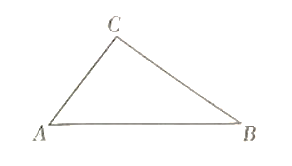
(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)求S△ADC: S△ADB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,求证:
,求证:![]() .
.

(2)类比探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() 点在边
点在边![]() 的延长线上,连接
的延长线上,连接![]() .请判断:①
.请判断:①![]() 的度数为_________.②线段
的度数为_________.②线段![]() 之间的数量关系是_________.
之间的数量关系是_________.
(3)问题解决:在(2)中,如果![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路有![]() 的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为
的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为![]() 公路的维修时,甲队比乙队少用6天
公路的维修时,甲队比乙队少用6天
(1)求甲乙两工程队每天能完成维修公路的长度分别是多少![]()
(2)若甲队的工程费用为每天2万元,乙队每天的工程费用为1.2万元,15 天后乙队另有任务,余下工程由甲队完成,请你判断能否在规定的工期完成且总费用不超过80万元
查看答案和解析>>
科目:初中数学 来源: 题型:
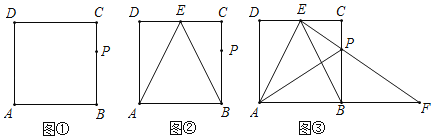
【题目】如图,在矩形ABCD中,AB═2,AD=![]() ,P是BC边上的一点,且BP=2CP.
,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条体下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
查看答案和解析>>
科目:初中数学 来源: 题型:
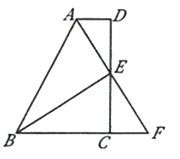
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,且
,且![]() 平分
平分![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() 是
是![]() 的平分线;
的平分线;
(4)探究![]() 和
和![]() 的面积间的数量关系,并写出探究过程.
的面积间的数量关系,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com