解:(1)令4x
2+8x-1=0,
∵a=4,b=8,c=-1,b
2-4ac=64+16=80>0,
∴x
1=

,x
2=

,
则4x
2+8x-1=4(x-

)(x-

);
(2)二次三项式2x
2-4x+7在实数范围内不能利用上面的方法分解因式,理由如下:
令2x
2-4x+7=0,
∵b
2-4ac=(-4)
2-56=-40<0,
∴此方程无解,
则此二次三项式不能用上面的方法分解因式;
(3)令mx
2-2(m+1)x+(m+1)(1-m)=0,
由此二次三项式能用上面的方法分解因式,即有解,
∴b
2-4ac=4(m+1)
2-4m(m+1)(1-m)≥0,
化简得:(m+1)[4(m+1)+4m(m-1)]≥0,即4(m+1)(m
2+1)≥0,
∵m
2+1≥1>0,∴m+1≥0,解得m≥-1,又m≠0,
则m≥-1且m≠0时,此二次三项式能用上面的方法分解因式.
分析:(1)令多项式等于0,得到一个一元二次方程,利用公式法求出方程的两解,代入ax
2+bx+c=a(x-x
1)(x-x
2)中即可把多项式分解因式;
(2)令二次三项式等于0,找出其中的a,b及c,计算出b
2-4ac,发现其值小于0,所以此方程无解,故此二次三项式不能利用上面的方法分解因式;
(3)因为此二次三项式在实数范围内能利用上面的方法分解因式,所以令此二次三项式等于0,得到的方程无解,即b
2-4ac小于0,列出关于m的不等式,求出不等式的解集即可得到m的取值范围.
点评:此题考查了分解因式,根的判别式及根与系数的关系,是一道阅读理解型题,这类题应题中所提供的文字材料中获得相关的信息,既有考查基础知识的又考查自学能力与探究能力的,信息量大,解题方法灵活,既注重最终结果,又注重理解过程,主要考查学生分析、归纳、抽象、类比的能力.本题要求学生弄清二次三项式在实数范围内能分解因式的前提是令二次三项式等于0时,得到的方程有解,即根的判别式大于等于0,此时可根据阅读材料中的方法进行分解因式.学生作第三问求m范围时应注意二次项系数不为0这个隐含条件.

 ,x1x2=
,x1x2= .∵
.∵
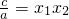 ,∴
,∴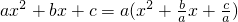 =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2). ,x2=
,x2= ,
, )(x-
)(x- );
);

 ,x1x2=
,x1x2= .
.
 ,
, =a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).
=a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2). ,x1x2=
,x1x2= .∵
.∵
 ,∴
,∴ =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).