
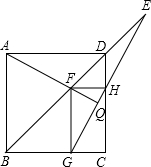
 已知:正方形ABCD中,F为BD上任意一点,过点F作FH⊥CD于点H,FG⊥BC于点G,连接AF并延长交GH于点Q,延长BD、GH交于点E.
已知:正方形ABCD中,F为BD上任意一点,过点F作FH⊥CD于点H,FG⊥BC于点G,连接AF并延长交GH于点Q,延长BD、GH交于点E.分析 (1)如图1中,连接AC交BD于点O,连接FC交GH于K.由△FBA≌△FBC,推出∠FAB=∠FCB,FA=FC,再证明∠AQE=90°,利用“8字型”证明∠E=∠FAO=∠FCO,利用∠QFK=∠FAO+∠FCO即可证明.
(2)如图2中,作GM⊥BD于M.易知△EMG是等腰直角三角形,设GM=MF=x,EF=y,GQ=4k,EQ=21k,构建方程组求出x与y的关系,可得y=6x,设FM=MG=a,则EF=6a,BM=a,BG=FG=$\sqrt{2}$a,求出FH、EH,再利用△BDK∽△EFH,推出$\frac{KB}{EG}$=$\frac{KD}{FH}$,推出$\frac{DK}{BD}$=$\frac{FH}{EH}$,由此即可解决问题.
解答 (1)证明:如图1中,连接AC交BD于点O,连接FC交GH于K.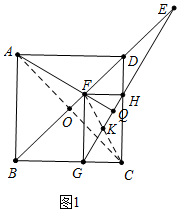
∵四边形ABCD是正方形,
∴BA=BC,∠FBA=∠FBC=45°,
在△FBA和△FBC中,
$\left\{\begin{array}{l}{AB=BC}\\{∠FBA=∠FBC}\\{BF=BF}\end{array}\right.$,
∴△FBA≌△FBC,
∴∠FAB=∠FCB,FA=FC,
∵FG⊥BC,FH⊥CD,
∴∠FGC=∠FHC=∠GCH=90°,
∴四边形FGCH是矩形,
∴KG=KC=KF=KH,
∴∠KCG=∠KGC,
∴∠KGC=∠FAB,
∵FG∥AB,
∴∠QFG=∠FAB=∠KGC,
∵∠KGC+∠FGQ=90°,
∴∠FGQ+∠QFG=90°,
∴∠FQG=∠FQE=90°=∠AOF,
∵∠AFO=∠EFQ,
∴∠E=∠FAO,
∵FA=FC,
∴∠FAO=∠FCO,
∵∠QFK=∠FAO+∠FCO,
∴∠QFK=2∠E.
(2)如图2中,作GM⊥BD于M.易知△EMG是等腰直角三角形,设GM=MF=x,EF=y,GQ=4k,EQ=21k,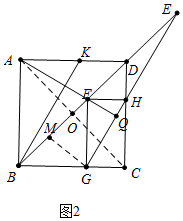
在Rt△EMG中,∵EM2+EG2=EG2,
∴(x+y)2+x2=625k2 ①
∵∠E=∠E,∠EQF=∠EMG,
∴△EQF∽△EMG,
∴$\frac{EQ}{EM}$=$\frac{EF}{EG}$,
∴y(y+x)=525k2 ②,
由①②消去k得到42x2+17xy-4y2=0,
∴(6x-y)(7x+4y)=0,
∴6x=y,设FM=MG=a,则EF=6a,BM=a,BG=FG=$\sqrt{2}$a,
∵FH∥BG,
∴$\frac{EF}{EB}$=$\frac{FH}{BG}$,
∴$\frac{6a}{8a}$=$\frac{FH}{\sqrt{2}a}$
∴FH=$\frac{3}{4}$$\sqrt{2}$a,GH=$\sqrt{F{G}^{2}+F{H}^{2}}$=$\frac{5\sqrt{2}}{4}$a,
∵$\frac{EF}{FB}$=$\frac{EH}{GH}$,
∴EH=$\frac{15\sqrt{2}}{4}$a,
∴$\frac{FH}{EH}$=$\frac{1}{5}$,
∵BK∥EG,
∴∠BDK=∠EFHG,∠KBD=∠E,
∴△BDK∽△EFH,
∴$\frac{KB}{EG}$=$\frac{KD}{FH}$,
∴$\frac{DK}{BD}$=$\frac{FH}{EH}$=$\frac{1}{5}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,学会利用参数解决问题,题目比较难,属于中考压轴题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
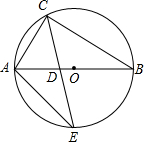 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,AC=2,CE平分∠ACB交⊙O于E,交AB于点D,连接AE.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,AC=2,CE平分∠ACB交⊙O于E,交AB于点D,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
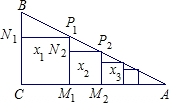 如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.
如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com