
| A. | 0或$\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
分析 分式方程去分母转化为整式方程,分整式方程无解和整式方程有解而分式方程无解两种情况讨论计算,分式方程无解确定出x的值,代入整式方程计算即可求出k的值,同时要考虑一元一次方程解的情况.
解答 解:去分母得:x+3=2kx,
∴(2k-1)x=3,
当k=$\frac{1}{2}$时,(2k-1)x=3无解,即原方程无解;
由分式方程无解,得到2x(x+3)=0,
解得:x=0或x=-3,
把x=0代入整式方程得:3=0,无解;
把x=-3代入整式方程得:-6k=0,解得:k=0,
综上所述,k的值为0或$\frac{1}{2}$.
故选A.
点评 此题考查了分式方程的解的情况,明确分式方程无解时,分母为0.


科目:初中数学 来源: 题型:解答题
 嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | 1-$\frac{3\sqrt{2}π}{16}$ | B. | $\sqrt{2}-\frac{3π}{8}$ | C. | 1-$\frac{3π}{8}$ | D. | $\frac{3π}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
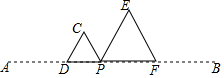 已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.
已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
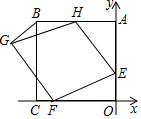 如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com