
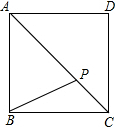
 已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.
已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程. 分析 PC2+PA2=2PB2,如图1,将△PAB绕点B顺时针旋转90°到△P′CB的位置,连接PP′.证明∠PCP′=∠BCP′+∠ACB=45°+45°=90°,利用勾股定理得到PC2+P′C2=PP′2,即PC2+AP2=PP′2,在Rt△PBP′中,利用勾股定理得到BP2+BP′2=PP′2,即2BP2=PP′2,所以PC2+AP2=2BP′2.
解答 解:PC2+PA2=2PB2,
如图1,将△PAB绕点B顺时针旋转90°到△P′CB的位置,连接PP′.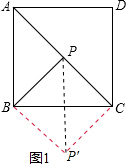
∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,
∴△PAB≌△P′CB,∠PBP′=90°,
∴BP=BP′,AP=P′C,∠BAP=∠BCP′,
∵四边形ABCD为正方形,
∴∠BAP=∠BCP=45°,
∴∠BCP′=45°,
∴∠PCP′=∠BCP′+∠ACB=45°+45°=90°,
∴PC2+P′C2=PP′2
∴PC2+AP2=PP′2,
在Rt△PBP′中,BP2+BP′2=PP′2,
∵BP=BP′,
∴2BP2=PP′2,
∴PC2+AP2=2BP′2.
点评 本题考查了正方形的性质、勾股定理,解决本题的关键是作出辅助线,将△PAB绕点B顺时针旋转90°到△P′CB的位置,连接PP′.


科目:初中数学 来源: 题型:选择题
 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m+1|+(m+6)的值为( )
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m+1|+(m+6)的值为( )| A. | 3 | B. | 5 | C. | 11-2$\sqrt{2}$ | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大为原来的2倍 | B. | 扩大为原来的4倍 | C. | 缩小为原来的2倍 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°,AD=3.5m,求∠B,∠C,∠BAD的度数和AB的长度.
如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°,AD=3.5m,求∠B,∠C,∠BAD的度数和AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
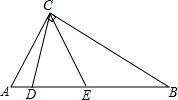 如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.
如图,在Rt△ABC中,AC=6,BC=8,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则△DCE的外接圆的半径是2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com