
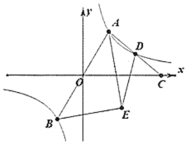
【题目】如图,过原点的直线与反比例函数![]() (
(![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限.点
在第一象限.点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .若
.若![]() 是线段
是线段![]() 中点,
中点,![]() 的面积为4,则
的面积为4,则![]() 的值为______.
的值为______.
【答案】![]()
【解析】
连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF;由AB经过原点,则A与B关于原点对称,再由BE⊥AE,AE为∠BAC的平分线,
可得AD∥OE,进而可得S△ACE=S△AOC;设点A(m,![]() ),由已知条件D是线段AC中点,DH∥AF,可得2DH=AF,则点D(2m,
),由已知条件D是线段AC中点,DH∥AF,可得2DH=AF,则点D(2m,![]() ),证明△DHC≌△AGD,得到S△HDC=S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=
),证明△DHC≌△AGD,得到S△HDC=S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() k+
k+![]() =8;即可求解;
=8;即可求解;
解:连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF,
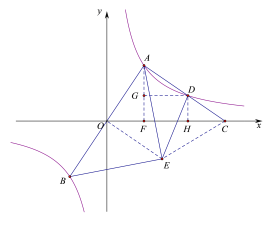
∵过原点的直线与反比例函数y=![]() (k>0)的图象交于A,B两点,
(k>0)的图象交于A,B两点,
∴A与B关于原点对称,
∴O是AB的中点,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE为∠BAC的平分线,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵D是线段AC中点,![]() 的面积为4,
的面积为4,
∴AD=DC,S△ACE=S△AOC=8,
设点A(m,![]() ),
),
∵D是线段AC中点,DH∥AF,
∴2DH=AF,
∴点D(2m,![]() ),
),
∵CH∥GD,AG∥DH,

∴∠ADG=∠DCH,∠DAG=∠CDH,
在△AGD和△DHC中,
∴S△HDC=S△ADG,
∵S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() ×(DH+AF)×FH+S△HDC
×(DH+AF)×FH+S△HDC
=![]() k+
k+![]() k+
k+![]() =8;
=8;
∴![]() k=8,
k=8,
∴k=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
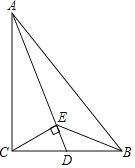
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.
(1)求证:BD2=DEAD;
(2)如果∠ABC=∠DCE,求证:BDCE=BEDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
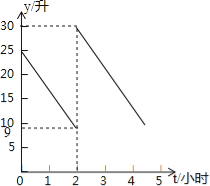
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.
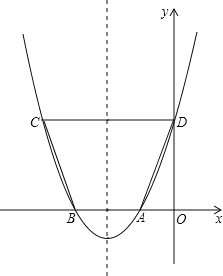
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日,“美丽玉环,文旦飘香”号冠名列车正式发车,为广大旅客带去“中国文旦之乡”的独特味道.根据市场调查,在文旦上市销售的30天中,其销售价格![]() (元公斤)与第
(元公斤)与第![]() 天之间满足函数
天之间满足函数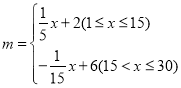 (其中
(其中![]() 为正整数);销售量
为正整数);销售量![]() (公斤)与第
(公斤)与第![]() 天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元.
天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元.
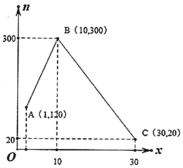
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在文旦上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额-日维护费)
天之间的函数关系式;(日销售利润=日销售额-日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
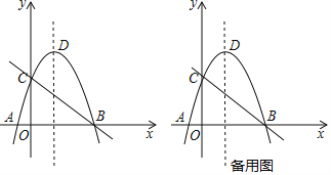
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
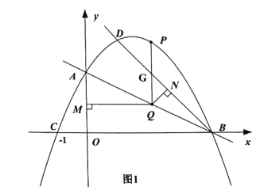
【题目】如图,一次函数![]() 的图像与坐标轴交于A、B两点,点C的坐标为
的图像与坐标轴交于A、B两点,点C的坐标为![]() ,二次函数
,二次函数![]() 的图像经过A、B、C三点.
的图像经过A、B、C三点.
(1)求二次函数的解析式
(2)如图1,已知点![]() 在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作
在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作![]() 轴于点M,作
轴于点M,作![]() 于点N,过Q作
于点N,过Q作![]() 轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足![]() ,求点E的坐标.
,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
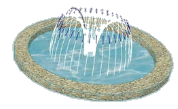
A.0.55米B.![]() 米C.
米C.![]() 米D.0.4米
米D.0.4米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com