
 如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.分析 (1)观察图形可确定:方法一,大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)2-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)2.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2-4mn=(m-n)2或(m+n)2=(m-n)2+4mn.
解答 解:(1)方法一:
∵大正方形的面积为(m+n)2,四个小长方形的面积为4mn,
∴中间阴影部分的面积为S=(m+n)2-4mn.
方法二:
∵中间小正方形的边长为m-n,∴其面积为(m-n)2.
(2)(m+n)2-4mn=(m-n)2或(m+n)2=(m-n)2+4mn.
点评 本题是完全平方式的实际应用,完全平方式经常与正方形的面积公式和长方形的面积公式联系在一起,要学会观察图形.


科目:初中数学 来源: 题型:选择题
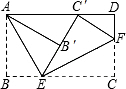 将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )
将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
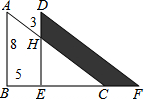 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7,24,25 | B. | 1.5,2,2.5 | C. | $\frac{5}{4}$,1,$\frac{3}{4}$ | D. | 40,50,60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
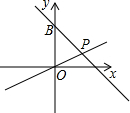 如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).
如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com