
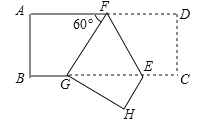
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
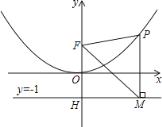
【题目】如图所示,二次函数图象的顶点在原点O,且经过点(1,![]() ).点F(0,1)在y轴上.直线y=-1与y轴交于点H.
).点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求该二次函数的解析式;
(2)设点P是(1)中图象上在第一象限内的动点,过点P作x轴的垂线与直线y=-1交于点M.
①求证:FM平分∠OFP;
②当△FPM是等边三角形时,试求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.

图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
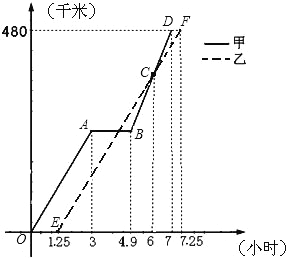
(1)由于汽车发生故障,甲组在途中停留了 小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组在学习二次根式时进行了如下题目的探索研究:
(1)填空![]() ;
;![]() ;
;
(2)观察第(1)题的计算结果回答:![]() 一定等于
一定等于
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .不确定
.不确定
(3)根据(1)、(2)的计算结果进行分析总结的规律,计算:![]() .
.
(4)请你参照数学兴趣小组的研究规律,化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:在图①的矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若∠1=∠2=∠3=∠4,则称四边形EFGH为矩形MNPQ的反射四边形.
操作与探究:在图②,图③的矩形ABCD中,AB=4,BC=8点E、F分别在BC、CD边上,试利用正方形网格分别作出两图中矩形ABCD的反射四边形EFGH,并求出每个反射四边形EFGH的周长.
发现与应用:由前面的操作可以发现一个矩形有不同的反射四边形,且这些反射四边形的周长都相等,若在图①矩形MNPQ中,MN=3,NP=4则其反射四边形EFGH的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
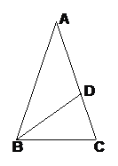
【题目】如图,已知△ABC中,D是AC边上一点,∠A=36,∠C=72,∠ADB=108。
求证:(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com