
【题目】阅读下面的文字,解答问题:
材料一:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:
如果![]() ,其中
,其中![]() 是整数,且
是整数,且![]() 那么
那么![]() .
.
材料二:已知![]() 是有理数,并且满足等式
是有理数,并且满足等式![]() 求
求![]() 的值.
的值.
解:![]()
![]()
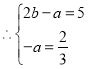 ,解得
,解得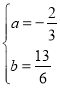
请解答:
(1)如果![]() ,其中
,其中![]() 是整数,且
是整数,且![]() 那么
那么![]() _______,
_______,![]() ______.
______.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值;
的值;
(3)已知![]() 是有理数,并且满足等式
是有理数,并且满足等式![]() ,求
,求![]() 的值.
的值.
【答案】(1)2,![]() -2;(2)-5;(3)9,-1.
-2;(2)-5;(3)9,-1.
【解析】
(1)根据夹逼法可得2<![]() <3,依此可求a和b;
<3,依此可求a和b;
(2)根据夹逼法可得3<![]() <4,依此可求m和n,代入可得结论;
<4,依此可求m和n,代入可得结论;
(3)因为x、y为有理数,所以x2-2y也是有理数,根据材料可得方程组,解出可解答.
解:(1)∵2<![]() <3,且
<3,且![]() =a+b,其中a是整数,且0<b<1,
=a+b,其中a是整数,且0<b<1,
∴a=2,b=![]() -2
-2
故答案为:2,![]() -2;
-2;
(2)∵3<![]() <4,
<4,
∴6+![]() 的小数部分为6+
的小数部分为6+![]() -9,即m=
-9,即m=![]() -3,
-3,
6-![]() 的整数部分为2,即n=2,
的整数部分为2,即n=2,
∴m-n-![]() =
=![]() -3-2-
-3-2-![]() =-5;
=-5;
(3)∵x2-2y-![]() y=17-4
y=17-4![]() ,
,
∵x,y是有理数,
∴ ,解得:
,解得:![]() ,
,
当x=5时,x+y=4+5=9,
当x=-5时,x+y=4-5=-1.


科目:初中数学 来源: 题型:
【题目】“单词的记忆效率“是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.如图描述了某次单词复习中小华,小红小刚和小强四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )

A. 小华B. 小红C. 小刚D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为 ![]() cm,AC=8cm,设运动时间为t秒.
cm,AC=8cm,设运动时间为t秒. 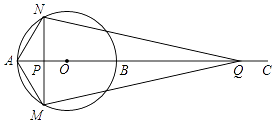
(1)求证:NQ=MQ;
(2)填空: ①当t=时,四边形AMQN为菱形;
②当t=时,NQ与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本上有这样一道例题:
例 已知等腰三角形底边长为a, 底边上的高的长为h,求作这个等腰三角.

作法:(1)作线段AB=a,
(2)作线段AB的垂直平分线MN,与AB相交于点D,
(3)在MN上取一点C,使DC=h,
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
请你思考只要CD垂直平分AB,那么△ABC就是等腰三角形的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 .
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的![]() ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
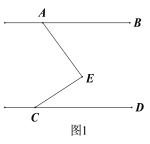
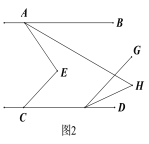
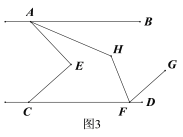
【题目】如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿射线CD平移至FG.
①如图2,若∠AEC=90°,FH平分∠DFG,求∠AHF的度数;
②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com