Question

填写理由或步骤
如图，已知AD∥BE，∠A=∠E
因为AD∥BE________．
所以∠A+________=180°________．
因为∠A=∠E（已知）
所以________+________=180°________．
所以DE∥AC________．
所以∠1=________．

Answer 1

（已知）    ∠ABE    （两直线平行，同旁内角互补）    ∠ABE    ∠E    （等量代换）    （同旁内角互补，两直线平行）    ∠2．（两直线平行，内错角相等）
分析：由已知的AD与BE平行，得到一对同旁内角互补，然后根据已知的两角相等，等量代换得到另一对同旁内角互补，根据同旁内角互补，两直线平行推出DE与AC平行，然后再根据两直线平行，内错角相等即可得证．
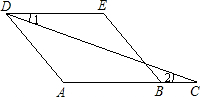
解答：如图，已知AD∥BE，∠A=∠E，
因为AD∥BE（已知）（1分）
所以∠A+∠ABE=180°（两直线平行，同旁内角互补）（2分）
因为∠A=∠E（已知）
所以∠ABE+∠E=180°（等量代换）（2分）
所以DE∥AC（同旁内角互补，两直线平行）（1分）
所以∠1=∠2（两直线平行，内错角相等）（2分）
故答案为：（已知）；∠ABE，（两直线平行，同旁内角互补）；∠ABE，∠E，（等量代换）；（同旁内角互补，两直线平行）；∠2，（两直线平行，内错角相等）
点评：此题考查了平行线的判定与性质，培养了学生发现问题，分析问题，解决问题的能力．解答此题的关键是注意平行线的性质和判定定理的综合运用．